第三节 FLUENT计算颤振导数

1、FLUENT UDF介绍

用户自定义函数（UDF）是用户自编的程序，可以动态地连接到FLUENT求解器上。UDF用C语言编写。使用DEFINE宏定义，其中可以使用标准的C语言库函数。UDF可以应用在以下场景中：

定制边界条件，定义材料属性等
在每次迭代的基础上调节计算值
方案初始化
后处理功能的改善
FLUENT湍流模型的改进

以一个设置入口边界轮廓信息的UDF代码为例简要介绍语法结构。

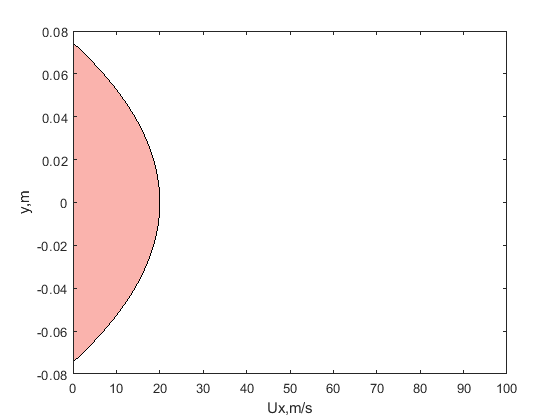
如需要在速度入口边界处定义一个抛物线形状的速度轮廓剖面： $U_x=20-20\times(\frac{y}{0.0745})^2 \tag{1}$ y坐标在入口中心处为(0,0)，在入口上部和下部分别为-0..0745m和0.0745m。入口中心处的x向速度为20m/s，边界上为0。

/***********************************************************************/
/*udfexample.c                                                         */
/*UDF for specifying a steady-state velocity profile boundary condition*/
/***********************************************************************/
#include "udf.h"
DEFINE_PROFILE(inlet_x_velocity,thread,index)
{
    real x[ND_ND];      /*this will hold the position vector*/
    real y;
    face_t f;
    begin_f_loop(f,thread)
    {
        F_CENTROID(x,f,thread);
        y = x[1];
        F_PROFILE(f,thread,index) = 20.-y*y/(.0745*.0745)*20.;
    }
    end_f_loop(f,thread)
}

上述代码解释为：

DEFINE_PROFILE宏的第一个变量表示速度入口处函数的名称，此处为inlet_x_velocity。在给定的边界区域上的所有单元面（face_t f）上将会使用这个函数。
第二个变量thread表示要在其上应用边界条件的线程的指针。
index标识要定义的变量的索引。当用户通过图形用户界面将UDF与边界条件对话框中的变量连接时，就设置了index。这个索引随后通过ANSYS Fluent求解器传递到UDF，以便函数知道操作哪个变量。
定义一些变量，real类型在单精度时为float，在双精度时为double float。x[ND_ND]中的ND_ND为一个宏，在3D时为3，在2D时为2。
begin_f_loop表示遍寻网格面，扫描所定义边界的所有网格面，对每个网格面都要赋值。值存储在F_PROFILE中。end_f_loop结束这个循环。
F_CENTROID表示读取每个网格面质心的坐标，并赋值给x。
F_PROFILE赋给每个网格面的数值与网格质心纵坐标的关系。

符合用户要求的速度入口边界条件设置完成。

2 、分状态单频强迫振动法求颤振导数理论

1.序言

颤振自激力模型

目前认为，颤振现象是由作用在结构上的自激力引起的。所谓自激力，是指作用在浸没于气流中的结构上的由其自身运动和气流相互作用而引起的气动力。

为了描述作用在桥梁结构上的自激力，研究人员提出了多种解析和经验模型。其中解析模型只能描述作用在薄机翼和理想薄平板上的自激力，而对于作用在实际桥梁结构上的自激力只能用经验模型来描述。

1971年，Scanlan和Tomko提出了一种理论与试验相结合的方法，他指出虽然对于非流线型的钝体不可能从基本的流体力学原理推导出解析气动力表达式，但可以通过专门设计的风洞试验测定在小振幅条件下的线性非定常气动力。Scanlan用6个颤振导数来描述作用于桥面上的气动自激升力和升力矩，并把自激力表示成结构运动竖向位移和扭转角以及它们的一阶导数的线性表达式。后来Huston将竖向位移$h$的影响考虑进去，得到了目前常见的含有8个颤振导数的气动自激升力和升力矩表达式： $L_{se}=\rho U^2B[K_hH_1^*\frac{\dot h}{U}+K_\alpha H_2^*\frac{B\dot \alpha}{U}+K_\alpha ^2H_3^*\alpha+K_h^2H_4^*\frac{h}{B}] \\ M_{se}=\rho U^2B^2[K_hA_1^*\frac{\dot h}{U}+K_\alpha A_2^*\frac{B\dot \alpha}{U}+K_\alpha ^2A_3^*\alpha+K_h^2A_4^*\frac{h}{B}] \tag{2}$ 式中， $B$ 为结构特征尺寸， $K=B\omega /U$ 为折算频率，颤振导数 $H_\text{i}^*\text{、}A_\text{i}^*(i=1,2,3,4)$ 是 $K$ 的无量纲函数。

近年来由于大跨度桥梁的发展，侧向位移的影响在风致振动分析中显得越来越重要，Sarkar和Jones等将自激力模型推广至三自由度，颤振导数也扩展为18个。

本文以Huston改进的Scanlan气动自激力为识别8个颤振导数的理论公式。

强迫振动法识别颤振导数

自由振动法识别颤振导数的试验设备简单，但颤振导数识别精度低，折减风速范围小，无法得到接近颤振临界风速时的颤振导数。

与自由振动识别方法相比，强迫振动法所需试验设备比较复杂，但具有可识别颤振导数的折减风速范围广、测试信号的信噪比高、可以直接识别作用在模型上的气动自激力、算法简单等优点。而对于数值模拟而言，强迫振动法无需复杂的试验设备，因此被广泛采用。

本文采用分状态单频强迫振动法，其中的分状态指的是结构振动分为纯扭转运动与纯竖向运动两种；单频指的是运动信号中只包含了一种频率。

有许多算法可以从得到的三分力数据中识别出颤振导数，这些算法可以按照分析信号的不同角度分为：频域方法和时域方法。

本节接下来将介绍分状态单频强迫振动法识别8个颤振导数的频域方法和时域方法。

不失一般性，选取结构做纯竖向运动的情况进行讨论。

2.频域识别方法

使结构做竖向小振幅的稳态简谐运动，即 $\tag{3} \alpha (t)=0,h(t)=h_0e^{i(\omega_ht+\phi_h)},p(t)\equiv0$ 式中 $h_0$ 为竖向振幅， $\omega _h$ 为竖向振动圆频率， $\phi_h$ 为竖向振动初始相位。

在此情况下，自激气动力可以描述为： $L_{se}(t)=Le^{i(\omega_ht+\phi_L)}\\ M_{se}(t)=Me^{i(\omega_ht+\phi_M)}\\ \tag{4}$ 同时将式(3)代入式(2)得： $L_{se}(t)=\rho U^2B[K_h^2H_1^*\frac{h}{B}i+K_h^2H_4^*\frac{h}{B}]\\ M_{se}(t)=\rho U^2B^2[K_h^2A_1^*\frac{h}{B}i+K_h^2A_4^*\frac{h}{B}] \tag{5}$ 由式(4)和式(5)，可以得到： $Le^{i(\omega_ht+\phi_L)}=\rho U^2B[K_h^2H_1^*\frac{h}{B}i+K_h^2H_4^*\frac{h}{B}]\\ Me^{i(\omega_ht+\phi_M)}=\rho U^2B^2[K_h^2A_1^*\frac{h}{B}i+K_h^2A_4^*\frac{h}{B}] \tag{6}$ 将上式两端分别进行傅里叶变换，有： $2\pi\delta(\omega-\omega_h)Le^{i\phi_L}=2\pi\delta(\omega-\omega_h)\rho U^2B[K_h^2H_1^*\frac{h_0}{B}i+K_h^2H_4^*\frac{h_0}{B}]e^{i\phi_h}\\ 2\pi\delta(\omega-\omega_h)Me^{i\phi_M}=2\pi\delta(\omega-\omega_h)\rho U^2B^2[K_h^2A_1^*\frac{h_0}{B}i+K_h^2A_4^*\frac{h_0}{B}]e^{i\phi_h} \tag{7}$ 两端的复数力在强迫振动频率 $\omega=\omega_h$ 处相等，有： $Le^{i(\phi_L-\phi_h)}=\rho U^2B[K_h^2H_1^*\frac{h}{B}i+K_h^2H_4^*\frac{h}{B}]\\ Me^{i(\phi_M-\phi_h)}=\rho U^2B^2[K_h^2A_1^*\frac{h}{B}i+K_h^2A_4^*\frac{h}{B}] \tag{8}$ 由上式可知，知道自激力的幅值和力与位移的相位差就可以得到相应的颤振导数值。

设 $F_L=Le^{i(\phi_L-\phi_h)},F_M=Me^{i(\phi_M-\phi_h)}$ ，即有： $H_1^*(K_h)=\frac{1}{\rho B^2h_0\omega_h^2}\text{Im}(F_L)\\ H_4^*(K_h)=\frac{1}{\rho B^2h_0\omega_h^2}\text{Re}(F_L)\\ A_1^*(K_h)=\frac{1}{\rho B^3h_0\omega_h^2}\text{Im}(F_M)\\ A_4^*(K_h)=\frac{1}{\rho B^3h_0\omega_h^2}\text{Re}(F_M) \tag{9}$ 同理，使结构做扭转小振幅的稳态简谐运动，可以得到： $H_2^*(K_\alpha)=\frac{1}{\rho B^3\alpha_0\omega_\alpha^2}\text{Im}(F_L)\\ H_3^*(K_\alpha)=\frac{1}{\rho B^3\alpha_0\omega_\alpha^2}\text{Re}(F_L)\\ A_2^*(K_\alpha)=\frac{1}{\rho B^4\alpha_0\omega_\alpha^2}\text{Im}(F_M)\\ A_3^*(K_\alpha)=\frac{1}{\rho B^4\alpha_0\omega_\alpha^2}\text{Re}(F_M) \tag{10}$ 关于自激力的提取

不管是试验还是数值模拟，采集得到的气动力中除了自激力外还存在其他周期性荷载如惯性力、周期性机械干扰、模型相对静止空气运动产生的气动力等。因此做出如下假定：强迫振动模型在特定风速下受到的动态力除自激气动力外其他周期性荷载与零风速下保持一致。即： $L_{se}(t)=L_{dy,U}(t)-L_{dy,0}(t)\\ M_{se}(t)=M_{dy,U}(t)-M_{dy,0}(t)\\ \tag{11}$ 由于节段模型即使在强迫简谐振动中，其振动时程信号也不是完全相同，因此不能够采用将所测得的动荷载时程信号按照对应相位相减的方法得到自激力，而是应该将足够长的动荷载时程信号转化到频域内，得到对应于振动频率 $\omega_h$ 的复数形式力（符号表示为 $F^{'}$ ）相减来得到自激力，即： $\text{Re}[L_{se}^{'}(\omega_h)]=\text{Re}[L_{dy}^{'}(\omega_h)]-\text{Re}[L_{dy,0}^{'}(\omega_h)]\\ \text{Im}[L_{se}^{'}(\omega_h)]=\text{Im}[L_{dy}^{'}(\omega_h)]-\text{Im}[L_{dy,0}^{'}(\omega_h)]\\ \text{Re}[M_{se}^{'}(\omega_h)]=\text{Re}[M_{dy}^{'}(\omega_h)]-\text{Re}[M_{dy,0}^{'}(\omega_h)]\\ \text{Im}[M_{se}^{'}(\omega_h)]=\text{Im}[M_{dy}^{'}(\omega_h)]-\text{Im}[M_{dy,0}^{'}(\omega_h)]\\ \tag{12}$ 至此，颤振自激力的提取、强迫振动法识别颤振导数的频域方法介绍完毕。

3.时域识别方法

首先，基于式(2)，令 $\begin{bmatrix} H_1\\ H_2\\ H_3\\ H_4 \end{bmatrix} =\rho U^2B \begin{bmatrix} \frac{K_h}{U}\\ & \frac{K_\alpha B}{U}\\ & & K_\alpha^2\\ & & & \frac{K_h^2}{B} \end{bmatrix} \cdot \begin{bmatrix} H_1^*\\ H_2^*\\ H_3^*\\ H_4^* \end{bmatrix} \tag{13}$

$\begin{bmatrix} A_1\\ A_2\\ A_3\\ A_4 \end{bmatrix} =\rho U^2B^2 \begin{bmatrix} \frac{K_h}{U}\\ & \frac{K_\alpha B}{U}\ & & K_\alpha^2\\ & & & \frac{K_h^2}{B} \end{bmatrix} \cdot \begin{bmatrix} A_1^*\\ A_2^*\\ A_3^*\\ A_4^* \end{bmatrix} \tag{14}$

则，式(2)变为： $L_{se}=H_1\dot h+H_2 \dot \alpha+H_3\alpha+H_4h\\ M_{se}=A_1\dot h+A_2 \dot \alpha+A_3\alpha+A_4h\\ \tag{15}$ 使结构做竖向小振幅的稳态简谐运动，即 $\alpha (t)=0,h(t)=h_0e^{i(\omega_ht+\phi_h)},p(t)\equiv0 \tag 3$ 式中 $h_0$ 为竖向振幅， $\omega _h$ 为竖向振动圆频率， $\phi_h$ 为竖向振动初始相位。

将式(3)带入式(15)得到： $L_{se}=H_1\dot h+H_4h\\ M_{se}=A_1\dot h+A_4h \tag{16}$ 上式也可以写成矩阵形式： $\mathbf{Q_{se}}=\mathbf{\Phi_h}\mathbf{D_h} \tag{17}$ 式中 $\mathbf{Q_{se}}$ 为单自由度竖向稳态简谐振动自激力矩阵。 $\mathbf{Q_{se}}= \begin{bmatrix} L_{se1} & M_{se1}\\ L_{se2} & M_{se2}\\ \vdots & \vdots\ L_{sen} & M_{sen}\\ \end{bmatrix} \tag{18}$

$\mathbf{\Phi_h}= \begin{bmatrix} \dot h_1 & h_1\\ \dot h_2 & h_2\\ \vdots & \vdots\\ \dot h_n & h_n\\ \end{bmatrix} \tag{19}$

$\mathbf{D_h}= \begin{bmatrix} H_1 & A_1\\ H_4 & A_4 \end{bmatrix} \tag{20}$

式中 $n$ 为一个采样样本所包含的数点数。

利用最小二乘法可以得到 $\mathbf{D_h}$ 的最小二乘估计值： $\mathbf{D_h}=(\mathbf{\Phi}_h^T\mathbf{\Phi_h})^{-1}\mathbf{\Phi_h^T}\mathbf{Q_se} \tag{21}$ 同理可以得到 $\mathbf{D_\alpha}$ 。利用式(13)和式(14)可以得到无量纲化的颤振导数 $H_\text{i}^*\text{、}A_\text{i}^*(i=1,2,3,4)$ 。

关于自激力的提取

时域方法与频域方法拥有相同的荷载假定：强迫振动模型在特定风速下受到的动态力除自激气动力外其他周期性荷载与零风速下保持一致。采用时域方法识别颤振导数时，传统的方法是将起始相位相同的特定风速下外力时程信号与零风速下外力时程信号相减得到自激力。即： $L_{se}(t)=L_{dy,U}(t)-L_{dy,0}(t)\\ M_{se}(t)=M_{dy,U}(t)-M_{dy,0}(t)\\ \tag {11}$ 对于试验而言，结构的振动并不是理想的稳态简谐振动，强迫振动装置本身的机械振动及外界振动都会作为噪声信号引入力信号及加速度信号中，这样无论是竖向、横向还是扭转振动，即使起始相位相同，各风速下加速度时程信号并非完全相等，惯性力(矩)等也不完全相等。因而采用起始相位相同的外力时程信号相减的方法获取自激力就会产生一定的误差。

而对于数值模拟，特定风速与零风速工况唯一差别即风速参数，其他参数可控制严格不变。因此时域传统的方法式(11)能直接应用，得到自激力信号。

至此，颤振自激力的提取、强迫振动法识别颤振导数的时域方法介绍完毕。

3、刚体单频强迫振动UDF文件(Forced_Vibration.c)

本节介绍的刚体单频强迫振动UDF文件。该文件适用于上文介绍的分状态单频率强迫振动求颤振导数理论。

1.刚体单频强迫振动UDF文件代码

#include "udf.h"
/*this function defines velocity of center of gravity for vertical and z_rotation*/
/*********************************************************/
/*                      监测壁面                         */
/*********************************************************/
real ZoneID=15;/*需要监测压力的运动边界ID，即壁面*/
/*********************************************************/
/*                        f1                             */
/*********************************************************/
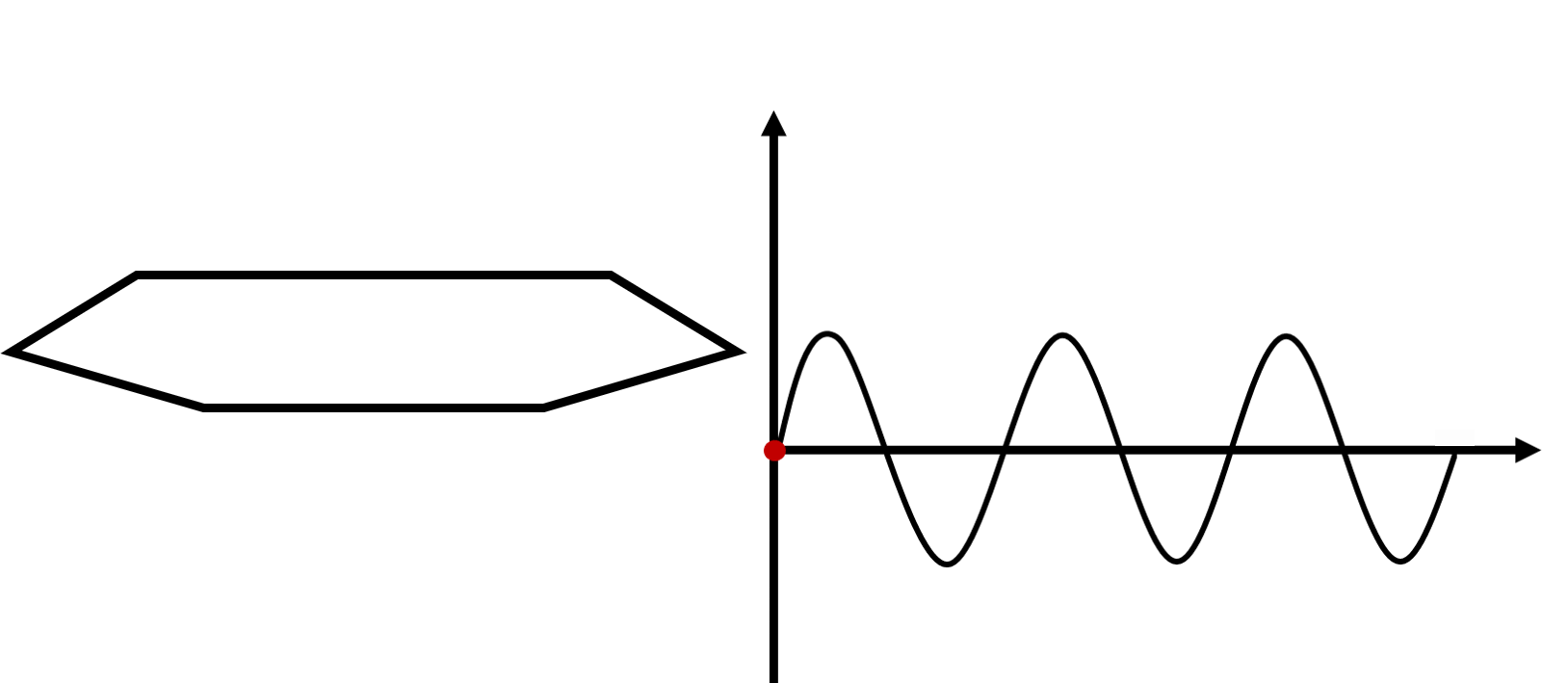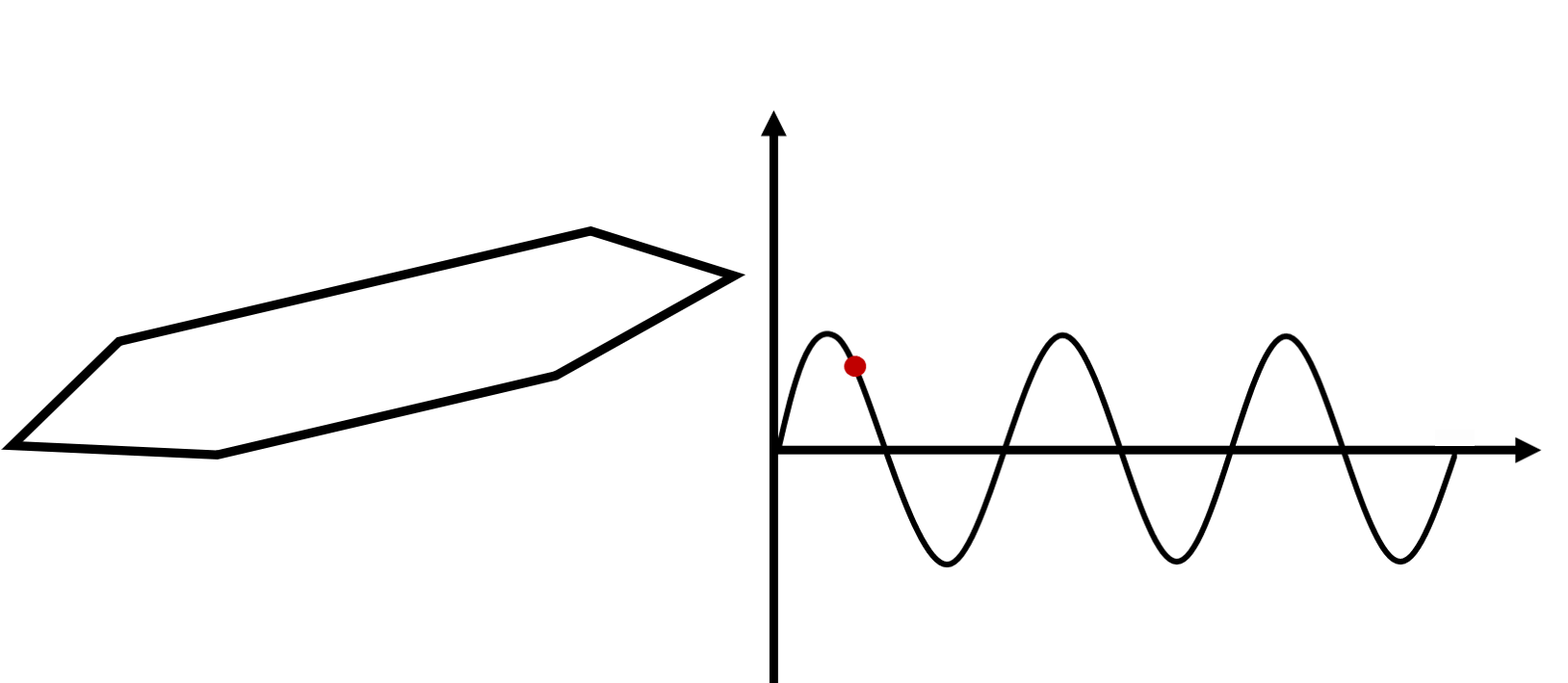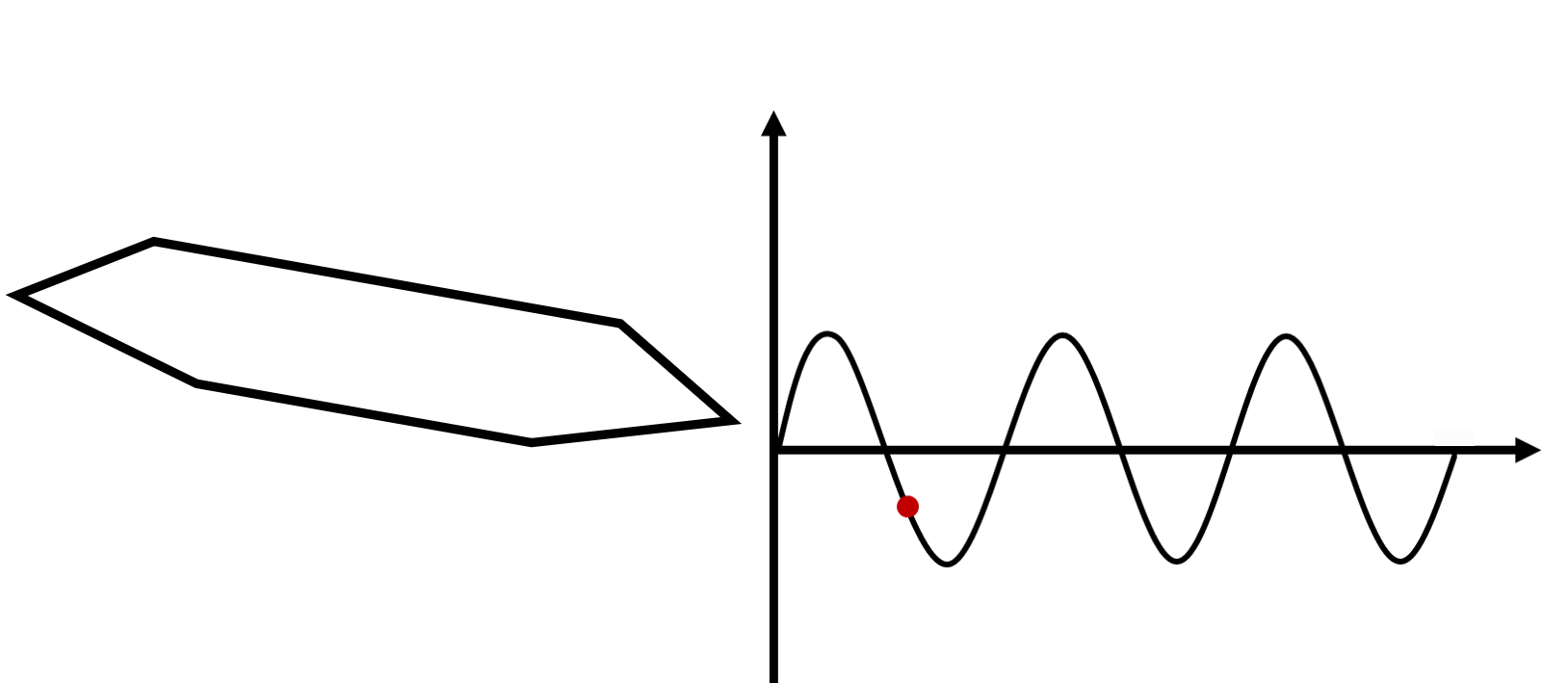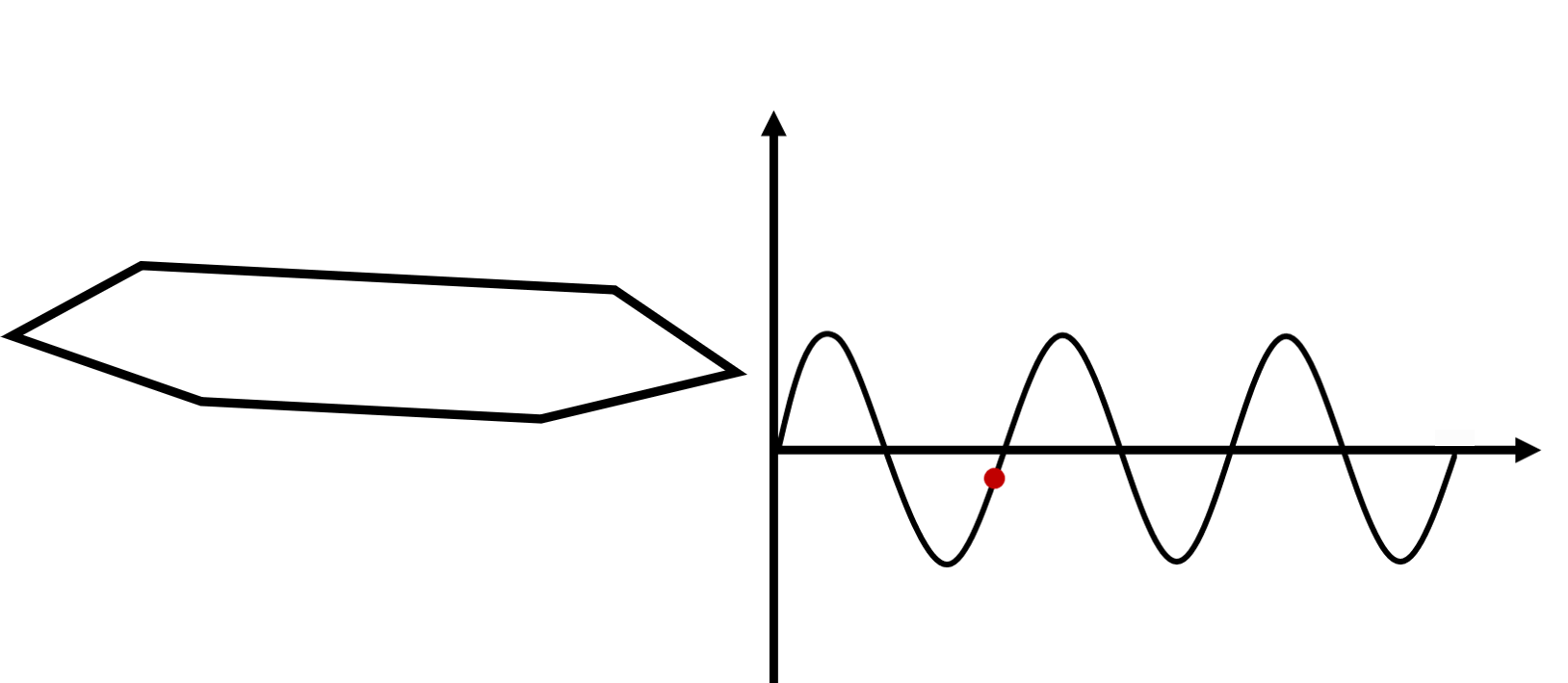
DEFINE_CG_MOTION(f1,dt,cg_vel,cg_omega,time,dtime)
{
    real f1=1.313;
    real h=0;
    /*h represents the amplitude of vertical motion h(normal)*/
    /*h should not be greater than 0.01*B*/
    real alpha=2;
    /*alpha represents the amplitude of z_rotational motion alpha(normal)*/
    /*alpha should not be greater than 2 degree*/
    real Vy,Omega_z,h,alph;
    real pi=3.1415926;
    Vy=h*2.0*pi*f1*cos(2.0*pi*f1*time);
    Omega_z=(alpha*pi/180)*2.0*pi*f1*cos(2.0*pi*f1*time);

    cg_vel[1]=Vy;
    cg_omega[2]=Omega_z;
}

代码解释如下：

DEFINE_CG_MOTION宏主要用于描述刚体的运动。以速度为描述对象。运动过程中部件几何形状不会发生任何改变，只是其质心位置发生改变。格式为DEFINE_CG_MOTION(name,dt,cg_vel,cg_omega,time,dtime)。主要返回值为cg_vel或cg_omega。
name为宏的名称，此处定义为f
dt为一个指针Dynamic_Thread *dt，存储动网格属性，通常不需要用户干预
cg_vel为平动速度数组，其中0，1，2索引表示x，y，z方向速度
cg_omega为转动速度数组，其中0，1，2索引表示x，y，z方向角速度
time为当前时间
dtime为时间步长

上述代码表示的刚体单频强迫振动运动示意如下：

4、结构强迫振动计算文件(Forced_Vibration.jou)

本节介绍的结构动网格计算文件设置适用于大部分结构做强迫振动情况，只需要修改少量参数即可完成设置。为完成不同的计算目的，部分代码应根据个人需求进行编写与补充。

1.Journal文件的功能组成

为实现计算流体流过做强迫振动运动的固体表面这种特定的流动状态，需要在FLUENT求解器中详细设置各个功能的开启与关闭状态，并且小心仔细地决定每个参数的取值。实现上述流动状态的Journal文件需要由以下几个功能块：

读入CASE文件(.cas)和DATA文件(.dat)
编译并装载UDF文件
切换为瞬态求解器
选择湍流模型
设置速度入口流动、壁面边界、压力出口流动等边界条件
设置动网格启动状态与参数
设置三分力系数的参考变量，如 $U\text{、}B$ 等
设置力或者系数的监控器
初始化流场
设置瞬态计算的时间步长和总步数
[可选]存储计算完成后的CASE文件和DATA文件

2.结构强迫振动计算文件代码

注：纯竖弯和纯扭转的代码在动网格设置上有所不同

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;                      纯竖弯强迫振动计算                    ;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;读入cas&data 
;;此处读入的时三分力计算后导出的CASE&DATA文件。经由三分力计算过后的流场状态更稳定
file/read-case/CASE1-3.cas
file/read-data/CASE1-3.dat

;;编译并装载UDF
/define/user-defined/compiled-functions/compile libudf yes Forced_Vibration.c "" ""
/define/user-defined/compiled-functions load libudf

;;稳态转瞬态，选择时已自动决定瞬态计算
define/models/unsteady-2nd-order
;;选择湍流模型，SST k-ω
define/models/viscous/kw-sst y
;;定义速度入口条件
;;其中的888表示入口速度U，应根据具体情况修改，其他参数可以不修改
define/boundary-conditions/velocity-inlet/inlet yes yes no 888 no 0 no 1 no 0 no no yes 1 10
define/boundary-conditions/pressure-outlet outlet yes no 0 no yes no no yes 1 10 yes no no

;;打开动网格并设置参数
define/dynamic-mesh/dynamic-mesh? yes no no no no
;;代码中的-0.04634为形心处位置
define/dynamic-mesh/zones/create mid_in rigid-body f1::libudf no 0 -0.04634 0
;;代码中的16表示圆形流域交界面外的网格ID
define/dynamic-mesh/zones/create interface_out rigid-body f1::libudf no no 0 -0.04634 0 16 constant 0 no no
define/dynamic-mesh/controls/smoothing? yes
define/dynamic-mesh/controls/smoothing-parameters/smoothing-method spring
define/dynamic-mesh/controls/smoothing-parameters/spring-on-all-elements? yes
define/dynamic-mesh/controls/remeshing? yes

;;投影面积和特征长度设置
report/reference-values/compute/velocity-inlet inlet
report/reference-values area 0.833
report/reference-values/ length 0.833
;;监视器设置
solve/monitors/residual/convergence-criteria 1e-3 1e-3 1e-3 1e-3 1e-3
solve/monitors/force/monitor-unsteady-iters? no
solve/monitors/force/set-drag-monitor cd-1 y wall () y y cd_f1 y 2 n 1 0
solve/monitors/force/set-lift-monitor cl-1 y wall () y y cl_f1 y 3 n 0 1
solve/monitors/force/set-moment-monitor cm-1 y wall () y y cm_f1 y 4 n 0 -0.04634 0 0 1
;;利用速度入口初始化流场
solve/initialize/compute-defaults/velocity-inlet inlet 
solve/initialize/initialize-flow ok
;;修改时间求解步长和时间步
solve/set/time-step 0.005
solve/set/number-of-time-steps 18000
;;求解，每一步内迭代80次
solve/dual-time-iterate 18000 350
;;存储最后一步
file/write-case-data/CASE1-4.cas
;;执行完结构强迫振动计算文件后，会得到计算完成后的CASE1-4文件。

纯扭转强迫振动计算的代码只需替换上述代码的动网格部分（22-31行）

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;                      纯扭转强迫振动计算                    ;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;打开动网格并设置参数
define/dynamic-mesh/dynamic-mesh? yes no no no no
;;代码中的-0.04634为形心处位置
define/dynamic-mesh/zones/create mid_in rigid-body f1::libudf no 0 -0.04634 0
define/dynamic-mesh/controls/smoothing? no

5、分状态单频强迫振动法求颤振导数的步骤

1.确定感兴趣的折算风速范围。如：

$\text{reducedVelocity}=\frac{U}{fB}=[2,4,6,8,10,12]$

2.确定结构单频强迫振动运动的频率。当速度为5m/s，特征尺寸为0.5m/s：

$f=\frac{U}{\text{redeucedVelocity}\times B}=\frac{10}{[2,4,6,8,10,12]}\text{Hz}$

3.采用批处理或其他方法，分状态计算确定来流条件下单频强迫振动的三分力

$1\text{取}h=h_0<0.01B,\alpha=0,\text{分别计算结构在}f=\frac{10}{[2,4,6,8,10,12]}\text{Hz六种频率强迫振动下的三分力}$

$2\text{取}h=0,\alpha=\alpha_0<2°,\text{分别计算结构在}f=\frac{10}{[2,4,6,8,10,12]}\text{Hz六种频率强迫振动下的三分力}$

以上共需要计算2×6=12种工况。每个工况采样的时间应大于10个对应的振动周期。

4.根据得到的三分力数据，采用时域或频域方法计算出给定折算风速下的颤振导数值。

$C_\text{D、}C_\text{L、}C_\text{M}\xrightarrow[frequency\text{ }domain\text{ }method]{time\text{ }domain\text{ }method}H_\text{i}^*\text{、}A_\text{i}^*(i=1,2,3,4)$

至此，利用FLUENT提供的UDF文件，结合分状态单频强迫振动法求颤振导数的理论，可以得到结构常用的8个颤振导数。

1.3 FLUENT计算颤振导数

第三节 FLUENT计算颤振导数

1、FLUENT UDF介绍

2 、分状态单频强迫振动法求颤振导数理论

3、刚体单频强迫振动UDF文件(Forced_Vibration.c)

4、结构强迫振动计算文件(Forced_Vibration.jou)

5、分状态单频强迫振动法求颤振导数的步骤

results matching ""

No results matching ""

第三节 FLUENT计算颤振导数

1、FLUENT UDF介绍

2 、分状态单频强迫振动法求颤振导数理论

3、 刚体单频强迫振动UDF文件(Forced_Vibration.c)

4、结构强迫振动计算文件(Forced_Vibration.jou)

5、分状态单频强迫振动法求颤振导数的步骤

results matching ""

No results matching ""

3、刚体单频强迫振动UDF文件(Forced_Vibration.c)