第四节 傅里叶变换的MATLAB实现

1、向量的离散傅里叶变换

参考MATLAB的描述，定义$Y=fft(X)$，当$X$是向量时，$Y$为该向量的傅里叶变换。

当信号$X$为长度为$n$的实信号时，由以下向量的离散傅里叶变换可知，返回值$Y$为复信号。 $$Y(k)=\sum_{j=1}^{n}X(j)W_n^{(j-1)(k-1)},k=1,2,\dots,n\\ W_n=e^{-i 2\pi/n} \tag{1}$$ 即，对于第$k$个$Y$信号，$Y(k)=a_k+ib_k=r_ke^{i\theta_k}$，其幅值为$r_k=\sqrt{a_k^2+b_k^2}$，其幅角满足$tan\theta_k=\frac{b_k}{a_k}\text{，当}a_k\ne0$。

而下式为复信号$Y$的傅里叶逆变换： $$X(j)=\frac{1}{n}\sum_{k=1}^nY(k)W_n^{-(j-1)(k-1)},j=1,2,\dots,n \tag{2}$$ 以下两个事实/问题需要了解，即①复信号Y(k)中的数据由一对对共轭复数组成；②这些复数的幅值和辐角含义。

对于事实①，有如下推导：

1°当$n$为奇数时，除去$Y(1)$为实数（又叫直流分量），其余数据两两共轭。 $$Y(1)=\sum_{j=1}^{n}X(j)\in \mathbf{R} \tag{3}$$

$$\begin{align} Y(n+1-k)&=\sum_{j=1}^{n}X(j)e^{(-i 2\pi)/n(j-1)(n-k)}\notag\\ &=\sum_{j=1}^{n}X(j)e^{i(j-1)(-2\pi +2\pi k/n)}\notag\\ &=\sum_{j=1}^{n}X(j)e^{i(j-1)(2\pi k/n)}\notag\\ &=\sum_{j=1}^{n}X(j)e^{i 2\pi/n(j-1)k}\notag\\ &=Y^*(k+1),k=1,2,\dots,n-1 \end{align} \tag{4}$$

2°当$n$为偶数时，除去$Y(1)、Y(\frac{n}{2}+1)$为实数（又叫直流分量），其余数据两两共轭。 $$\begin{align} Y(\frac{n}{2}+1)&=\sum_{j=1}^{n}X(j)e^{-2i \pi/n(j-1)\frac{n}{2}}\notag\\ &=\sum_{j=1}^{n}X(j)e^{-i \pi (j-1)}\in \mathbf{R}\\ \end{align} \tag{5}$$ 对于问题②，由傅里叶逆变换： $$nX(j)=\sum_{k=1}^nY(k)e^{2i \pi/n(j-1)(k-1)}\\ \tag{6}$$ 考虑共轭的两个数据$Y(m)=a+ib$与$Y(n+2-m)=a-ib$，则 $$\begin{align} Y(m)+Y(n+2-m)&=(a+ib)e^{2i \pi/n(j-1)(m-1)}+(a+ib)e^{2i \pi/n(j-1)(n+1-m)}\notag\\ &=2acos[2\pi /n(j-1)(m-1)]-2bsin[2\pi /n(j-1)(m-1)]\notag\\ &=Acos[2\pi /n(j-1)(m-1)+\phi] \tag{7} \end{align}$$ 式中，$A=2\sqrt{a^2+b^2}$，$tan\phi=\frac{b}{a}$，当$a\ne0$时。

所以原来的实信号$nX(j)$可以表示为：

1°当$n$为奇数时， $$nX(j)=Y(1)+A_2cos[2\pi /n(j-1)+\phi_2]+\dots\\ +A_{\frac{n+1}{2}}cos[2\pi /n(j-1)({\frac{n+1}{2}}-1)+\phi_{\frac{n+1}{2}}] \tag{8}$$ 2°当$n$为偶数时， $$nX(j)=Y(1)+A_2cos[2\pi /n(j-1)+\phi_2]+\dots\\ +A_{\frac{n}{2}}cos[2\pi /n(j-1)({\frac{n}{2}}-1)+\phi_{\frac{n}{2}}]+Y(\frac{n}{2}+1)e^{i \pi (j-1)} \tag{9}$$ 此时可以发现，原实信号$X(j)$频率分量组成的强度与相位角由复信号$Y(k)$的幅值和辐角表示。

• 关于频率分量的组成

  设采样频率为$f_s$，则离散信号$X(j)$与连续信号$x(t)$的联系为$X(j)=x(t=\frac{j-1}{f_s})$。以$n$为偶数时为例有： $$nX(j)=x(t=\frac{j-1}{f_s})=Y(1)+A_2cos[2\pi /nf_st+\phi_2]+\dots\\ +A_{\frac{n}{2}}cos[2\pi /nf_st({\frac{n}{2}}-1)+\phi_{\frac{n}{2}}]+Y(\frac{n}{2}+1)e^{i \pi f_st},t=\frac{j-1}{f_s} \tag{10}$$ 上式说明，原信号中的频率分量的组成为 $$0、\frac{1}{n}f_s、\frac{2}{n}f_s、\dots、(\frac{1}{2}-\frac{1}{n})f_s \tag{11}$$ 这说明，当采样频率为$f_s$时，在频域内最多只能不失真地采样到最大为$f_s/2$的频率。这即为奈奎斯特采样定理：在进行模拟/数字信号的转换过程中，当采样频率$f_s$大于信号中最高频率$f_{max}$的2倍时，采样之后的数字信号完整地保留了原始信号中的信息。

• 关于频率分量的组成的强度与相位角

  由式(9)和式(7)可以得到，原实信号$X(j)$频率分量组成的强度与相位角可以由前$\frac{n+2-mod(n,2)}{2}$个复信号$Y(k)$的幅值和辐角表示。

  即$nX(j)$中频率分量的强度为前$\frac{n+2-mod(n,2)}{2}$个复信号$Y(k)$的幅值×2（直流分量除外）；

  $nX(j)$中频率分量的相位角与前$\frac{n+2-mod(n,2)}{2}$个复信号$Y(k)$的辐角一致。

2、MATLAB傅里叶变换简要介绍

MATLAB内关于傅里叶变换的介绍可以参考其官方支持文档：傅里叶变换 - MATLAB & Simulink - MathWorks 中国

该文档简要介绍了：

• 离散傅里叶变换基本原理
• 内置函数fft，fftshift等的使用
• 含噪信号清除随机噪声并显现频率
• 提高计算效率

3、MATLAB官方fft函数介绍

MATLAB内关于fft函数的介绍可以参考其官方支持文档：快速傅里叶变换 - MATLAB fft - MathWorks 中国

下面截取一部分简单展开介绍。

Fs = 1000;            % Sampling frequency                    
T = 1/Fs;             % Sampling period       
L = 1500;             % Length of signal
t = (0:L-1)*T;        % Time vector

% Form a signal containing a 50 Hz sinusoid of amplitude 0.7 and a 120 Hz sinusoid of amplitude 1.
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
% Compute the two-sided spectrum P2. Then compute the single-sided spectrum P1 based on P2 and the even-valued signal length L.
Y = fft(S);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
% Define the frequency domain f and plot the single-sided amplitude spectrum P1. 
f = Fs*(0:(L/2))/L;
plot(f,P1) 
title('Single-Sided Amplitude Spectrum of S(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')

上述代码进行了几项操作：

• 构造一个信号，其中包含幅值为 0.7 的 50 Hz 正弦量和幅值为 1 的 120 Hz 正弦量。
• 计算信号的傅里叶变换。
• 计算双侧频谱P2。然后基于P2和偶数信号长度L计算单侧频谱P1。
• 定义频域f并绘制单侧幅值频谱P1。

可以看到MATLAB内置函数$Y=fft(X)$只是完成了式(1)的变换，返回值$Y$为复信号。并没有给出原信号的频率分量、频率分量强度以及频率分量相位角。而这些参数是实际问题需要考虑和研究的对象。因此可以重写fft函数，使其满足实际问题的需要，返回原信号的频率分量、频率分量强度以及频率分量相位角等参数。

4、重写fft函数

本节给出一个fft函数（fft1.m）的重写例子，具体情况可以根据个人需要删除、更改或添加。

function [fx,mag,phi] = fft1(data_x,freq,varargin)
    %正频域傅里叶变换
    %   data_x为数据时程,列向量
    %   freq为采样频率,单位为Hz
    %   fx,mag,phi分别为频率分量以及对应的幅值和辐角
    if nargin == 2
        wintype = 'rec';%默认为矩形窗
    elseif nargin == 3
        wintype = varargin{1};
    else
        disp('输入有误');
    end
    %%窗函数的定义
    switch wintype
        case 'han'
            w=hann(length(data_x));r=2;%汉宁窗,能量系数为2
        case 'ham'
            w=hamming(length(data_x));r=1.852;%海明窗,能量系数为1.852
        case 'tri'
            w=triang(length(data_x));r=2;%三角窗,能量系数为2
        case 'gau'
            w=gausswin(length(data_x));r=2.396;%高斯窗,能量系数为2.396
        case 'bkm'
            w=blackman(length(data_x),'periodic');r=2.381;%布莱克曼窗,能量系数为2.381
        case 'kai'
            w=kaiser(length(data_x),3*pi);r=2.48;%凯泽-贝塞尔窗,能量系数为2.48
        case 'ftw'
            w=flattopwin(length(data_x),'periodic');r=4.5455;%平顶窗,能量系数为4.5455
        otherwise
            w=1;r=1;%矩形窗,能量系数为1
    end
    %%向量按照列向量排布
    if size(data_x,1)==1
        data_x=data_x';
    end
    %%傅里叶变换
    data_x=data_x.*w;%时程上加窗函数
    y=fft(data_x)*2/length(data_x);%得到复信号y,×2表示负频域向正频域折叠
    phi=angle(y)/pi*180;%复信号y的辐角
    y_mag=abs(y);y_mag=y_mag*r;%复信号y的幅值， ×r表示考虑能量系数r

    fx=[0:freq/length(data_x):freq/2];%采样定理决定频率区间
    mag=mag(1:length(fx));%频率区间对应的幅值
    phi=phi(1:length(fx));%频率区间对应的辐角
end

值得指出的是，$cos(\omega t)$的辐角为0°，$sin(\omega t)$的辐角为-90°。

以上代码加入了窗函数。关于离散傅里叶变换窗函数与信号泄漏问题，可以参考什么是窗函数? - 知乎 (zhihu.com)等网页介绍。

窗函数部分的代码可以不封装在fft1.m函数内，根据实际使用情况来决定与使用。

下面给出一个实际例子，以检测重写的fft1.m函数的功能。

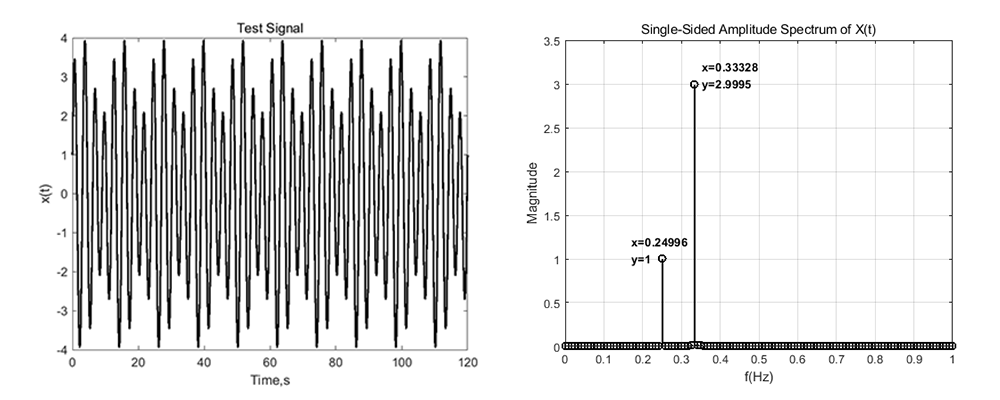
%%构造信号
fs=50;%采样频率50Hz
time=0:1/fs:120;%采样时间120s
x=cos(2*pi*1/4.*time)+3*sin(2*pi*1/3.*time);%构造信号，幅值分别为1和3，频率分别为1/4和1/3Hz
figure(1)
plot(time,x,'-k','LineWidth',1.5)
xlabel('Time,s')
ylabel('x(t)')
title('Test Signal')

[fx,mag,phi]=fft1(x,fs);%傅里叶变换

figure(2)
stem(fx,mag,'-k','LineWidth',1.5)
xlim([0 1])
grid on
xlabel('f(Hz)')
ylabel('Magnitude')
title('Single-Sided Amplitude Spectrum of X(t)')

i=find(abs(fx-1/4)*4<0.05);Cp_mag=max(mag(i));
phi1=phi(find(mag==Cp_mag))%显示频率成分对应的相位角

i=find(abs(fx-1/3)*3<0.05);Cp_mag=max(mag(i));
phi2=phi(find(mag==Cp_mag))%显示频率成分对应的相位角

运行后结果如下：

phi1=0.8017
phi2=-88.8084

至此，更贴近解决实际问题的MATLAB-FFT函数重写完成。