第五节 MATLAB处理气动力数据

1、静力三分力系数

本文中采取的案例如下：

B（桥面宽） H（高） b（风嘴伸出长度） α\alpha （风嘴角度） β\beta（斜腹板角度） i（桥面横坡） 缩尺比 U风速 Re雷诺数
46.68 5.83 1.66 63 18 0.02 1：60 3.5 2E5

注：表中长度单位为m，角度单位为°，速度单位为m/s

Section

采用POINTWISE划分网格，FLUENT进行静力三分力的求解。最后输出三分力系数文件cd_mean.out，cl_mean.out，cm_mean.out。

对于三分力（系数）结果，可采用MATLAB进行数据的读取与曲线的绘制。必要时可以进行傅里叶变换，对旋涡脱落频率进行监控。

以下展示MATLAB读取文件、绘制曲线并进行傅里叶变换的代码。使用时可以根据个人需求进行删除、更改和添加。

clc
clear
format short
%% Parameter Settings
Cdfolder='D:\cd_mean.out';
Clfolder='D:\cl_mean.out';
Cmfolder='D:\cm_mean.out';
data_length=10000;
max_freq=15;%傅里叶变换后绘图使用的最大频率值
B=50;H=5.83;%断面宽度为B，高度为H

%%读取数据文件
delimiterIn = ' '; %字符分隔符
headerlinesIn = 4;   %文件头的行数
imdata = importdata(Cdfolder, delimiterIn, headerlinesIn);
imdata=imdata.data;%结构类型数据的访问
time=imdata(end-data_length+1:end,2);%时间
Cd=imdata(end-data_length+1:end,3)*B/H;%阻力系数，因为FLUENT内阻力系数以宽度B为参考，此处转换为以高度H为参考
imdata = importdata(Clfolder, delimiterIn, headerlinesIn);
imdata=imdata.data;
Cl=imdata(end-data_length+1:end,3);%升力系数
imdata = importdata(Cmfolder, delimiterIn, headerlinesIn);
imdata=imdata.data;
Cm=imdata(end-data_length+1:end,3);%升力矩系数

meanC=[mean(Cd),mean(Cl),mean(Cm)]%输出三分力平均值
%%时域内绘图
subplot(321);
plot(time,Cd,'-k','LineWidth',1.5);
grid on
xlabel('Time,s');
ylabel('Cd');
subplot(323); 
plot(time,Cl,'-k','LineWidth',1.5);
grid on
xlabel('Time,s');
ylabel('Cl');
subplot(325);
plot(time,Cm,'-k','LineWidth',1.5);
grid on
xlabel('Time,s');
ylabel('Cm');
%%频域内绘图
subplot(322);
[fx,mag,phi]=fft1(Cd-mean(Cd),1/(time(2)-time(1)),'han');
stem(fx,mag,'-k','LineWidth',1.5);
xlabel('f(Hz)');
ylabel('Magnitude');
xlim([0,max_freq])
subplot(324);
[fx,mag,phi]=fft1(Cl-mean(Cl),1/(time(2)-time(1)),'han');
stem(fx,mag,'-k','LineWidth',1.5);
xlabel('f(Hz)');
ylabel('Magnitude');
xlim([0,max_freq])
subplot(326);
[fx,mag,phi]=fft1(Cm-mean(Cm),1/(time(2)-time(1)),'han');
stem(fx,mag,'-k','LineWidth',1.5);
xlabel('f(Hz)');
ylabel('Magnitude');
xlim([0,max_freq])

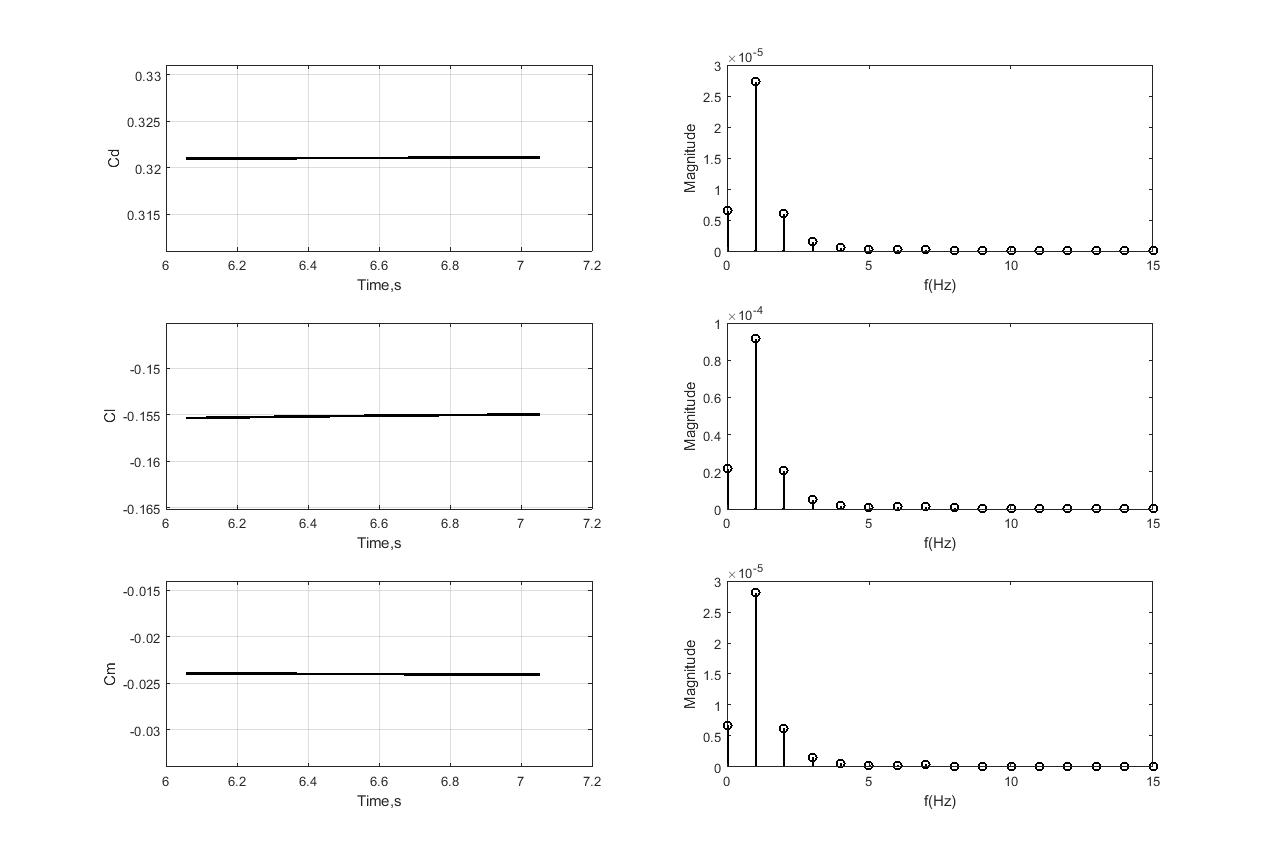
上述代码输出的结果如下：

meanC =  0.3211   -0.1551   -0.0240

Aero Coefficients

2、颤振导数Theodorsen理论解

1、Theodorsen平板气动自激力理论解

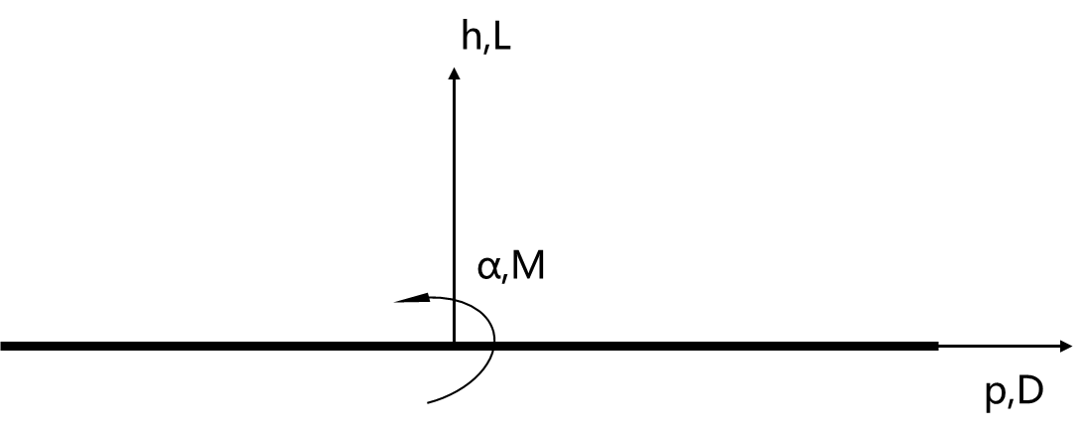
一块宽度为B，厚度为0，长度无限的直平板称为理想平板。假定某种原因，平板本身产生了竖向与扭转的小幅振动，横向振动暂时忽略。运动体系以及力的坐标定义如下图所示。

Plate Coordinates

Theodorsen1935年利用位势理论，证明了平板本身的微振动扰动了平板上、下表面的气流，扰动的气流反过来产生作用于平板的气动力，这个随时间变化的气动力与平板振动的速度、位移有关。如果平板作频率为ω\omega的简谐运动，即： h=h0cos(ωt)α=α0cos(ωt) h=h_0cos(\omega t)\\ \alpha = \alpha_0cos(\omega t) 则，Theodorsen导出的平板气动自激力的理论解为： L=πρb{−bh¨−2UC(k)h˙−[1+C(k)]Ubα˙−2U2C(k)α}M=πρb2{UC(k)h˙−b2α¨8+[−12+12C(k)]Ubα˙+U2C(k)α} L=\pi \rho b\{-b\ddot h -2UC(k)\dot h -[1+C(k)]Ub\dot \alpha -2U^2C(k)\alpha\}\\ M=\pi \rho b^2\{UC(k)\dot h -\frac{b^2\ddot \alpha}{8}+[-\frac12+\frac12C(k)]Ub\dot\alpha+U^2C(k)\alpha\} 式中，L、ML\text{、}M分别为单位长度的升力与扭矩；ρ\rho为空气密度；bb为薄平板半宽，板宽B=2bB=2b；UU为空气来流速度；h、αh\text{、}\alpha分别为截面竖向位移与扭转角；kk为无量纲折算频率k=bω/Uk=b\omega/U；ω\omega为振动圆频率；C(k)C(k)为Theodorsen循环函数，其表达式为： C(k)=H1(2)(k)H1(2)(k)+i⋅H0(2)(k)=F(k)+i⋅G(k) C(k)=\frac{H_1^{(2)}(k)}{H_1^{(2)}(k)+i\cdot H_0^{(2)}(k)}=F(k)+i\cdot G(k) 上式中，Hx(2)(k)H_x^{(2)}(k)是第二类xx阶汉克尔（Hankel）函数。汉克尔函数被定义为Hx(2)(k)=Jx−iYxH_x^{(2)}(k)=J_x-iY_x，JxJ_x和YxY_x分别为第一类和第二类贝塞尔（Bessel）函数。

  1. Scanlan自激力模型的Theodorsen循环函数表达式

对于机翼或者二维理想平板，Scanlan自激力模型可用Theodorsen循环函数的实部和虚部表示： H1∗=−πF(k)KH2∗=−π4K(1+F(k)+4G(k)K)H3∗=−πK2(F(k)−KG(k)4)H4∗=π(14+G(k)K)A1∗=π4F(k)KA2∗=π(F(k)−1)16K+πG(k)4K2A3∗=π128+πF4K2−πG16KA4∗=−πG(k)4K \begin{align} H_1^*&=-\pi\frac{F(k)}{K}\notag\\ H_2^*&=-\frac{\pi}{4K}(1+F(k)+\frac{4G(k)}{K})\notag\\ H_3^*&=-\frac{\pi}{K^2}(F(k)-\frac{KG(k)}{4})\notag\\ H_4^*&=\pi(\frac14+\frac{G(k)}{K})\notag\\ A_1^*&=\frac{\pi}{4}\frac{F(k)}{K}\notag\\ A_2^*&=\frac{\pi(F(k)-1)}{16K}+\frac{\pi G(k)}{4K^2}\notag\\ A_3^*&=\frac{\pi}{128}+\frac{\pi F}{4K^2}-\frac{\pi G}{16K}\notag\\ A_4^*&=-\frac{\pi G(k)}{4K} \end{align} 上式注意F和G函数的自变量为以半宽定义的k而非全宽定义的K。

将上述公式在MATLAB中实现，Theodorsen.m代码如下：

function [H,A] = Theodorsen(reduced_U)
    % Theodorsen非定常气动力
    % reduced_U为折算风速向量
    % H为Scanlan自激力颤振导数，以[H1,H2,H3,H4]排列
    % A为Scanlan自激力颤振导数，以[A1,A2,A3,A4]排列

    % 向量按照列向量排布
    reduced_freq=1./reduced_U;
    if size(reduced_freq,1)==1
        reduced_freq=reduced_freq';
    end
    %% Theodorsen循环函数
    K=2*pi*reduced_freq;% 折算圆频率
    k=K/2;
    C=besselh(1,2,k)./(besselh(1,2,k)+besselh(0,2,k)*complex(0,1));
    F=real(C);% Theodorsen函数的实部
    G=imag(C);% Theodorsen函数的虚部
    %% Scanlan颤振导数
    % 颤振导数H与A
    H=[-pi.*F./K,-pi/4./K.*(1+F+4*G./K),-pi./K.^2.*(F-K.*G/4),pi.*(1/4+G./K)];
    A=[pi/4./K.*F,pi*(F-1)/16./K+pi*G/4./K./K,pi/128+pi*F/4./K./K-pi*G/16./K,-pi*G/4./K];
end

当输入一组折算风速向量后，会得到对应的Scanlan自激力模型中的颤振导数值。

如：reducedU=[1,2,3,4,5,6,7,8,9,10]reduced U=[1,2,3,4,5,6,7,8,9,10]，输出结果绘图如下：

Theodorsen(1)Theodorsen(2)

Theodorsen(3)Theodorsen(4)

3、颤振导数识别（分状态单频强迫振动法）

本节讨论分状态单频强迫振动法求颤振导数在MATLAB中实现。具体理论见《第三节 FLUENT计算颤振导数》。

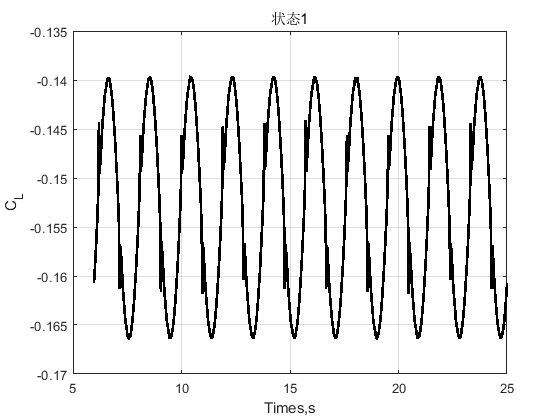
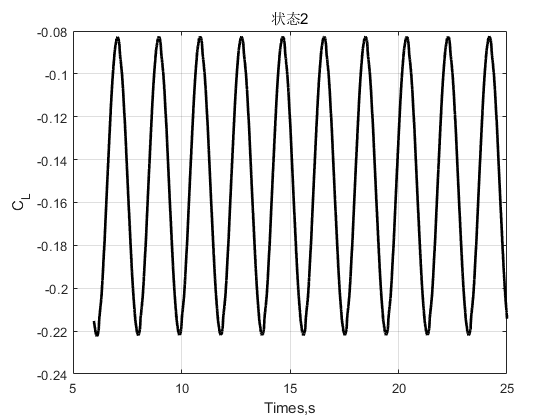
同静力三分力计算采用的案例，利用UDF文件与FLUENT得到该断面在折算风速为8时的三分力数据，即reducedU=8,f=0.5252Hzreduced U=8,f=0.5252\text{Hz}。让结构做分状态强迫振动： 状态1：h=0.004sin(2πft),α=0,f=0.5252Hz状态2：h=0,α=π180sin(2πft),f=0.5252Hz \begin{align} 状态1\text{：}h&=0.004sin(2\pi ft),\alpha=0,f=0.5252\text{Hz}\notag\\ 状态2\text{：}h&=0,\alpha=\frac{\pi}{180} sin(2\pi ft),f=0.5252\text{Hz} \end{align} 采样时间应确保至少包含10个振动周期。由此得到的三分力数据绘制如下：

注1：升力系数曲线均值不为零的原因为：模型上下不对称或来流相对模型振动的平衡位置攻角不为零。此时气动力将包含静力分量。因此在计算颤振导数之前，应将气动力数据进行零均值化处理。

注2：升力系数曲线存在一些尖刺点，原因不明，可能为网格质量不佳或是动网格设置问题导致。但是尖刺点不影响后续的颤振导数识别。

State1-1State1-2

State1-3State1-4

State2-1State2-2

State2-3State2-4

理论上应当再计算一次零风速下的三分力数据，在折算风速数据中扣除零风速的数据才为真实的自激力数据。但是本文仍以折算风速下采集得到的数据为自激力数据进行颤振导数的识别。因为只是演示MATLAB实现方法，因此由此造成误差不被讨论。

接下来采用频域方法和时域方法识别该断面在折算风速为8时的8个颤振导数$H\text{i}^*、A\text{i}^*(i=1,2,3,4)$

  1. 频域方法

由《第三节 FLUENT计算颤振导数》中的理论可知，频域方法需要的是三分力的幅值和力与对应位移的相位差。

设FL=12ρU2BCL=Lei(ϕL−ϕh),FM=12ρU2B2CM=Mei(ϕM−ϕh)F_L=\frac12\rho U^2BC_L=Le^{i(\phi_L-\phi_h)},F_M=\frac12\rho U^2B^2C_M=Me^{i(\phi_M-\phi_h)}，即有： H1∗(Kh)=1ρB2h0ωh2Im(FL)=U22Bh0ωh2Im(CL)H4∗(Kh)=1ρB2h0ωh2Re(FL)=U22Bh0ωh2Re(CL)A1∗(Kh)=1ρB3h0ωh2Im(FM)=U22Bh0ωh2Im(CM)A4∗(Kh)=1ρB3h0ωh2Re(FM)=U22Bh0ωh2Re(CM) H_1^*(K_h)=\frac{1}{\rho B^2h_0\omega_h^2}\text{Im}(F_L)=\frac{U^2}{2Bh_0\omega_h^2}\text{Im}(C_L)\\ H_4^*(K_h)=\frac{1}{\rho B^2h_0\omega_h^2}\text{Re}(F_L)=\frac{U^2}{2Bh_0\omega_h^2}\text{Re}(C_L)\\ A_1^*(K_h)=\frac{1}{\rho B^3h_0\omega_h^2}\text{Im}(F_M)=\frac{U^2}{2Bh_0\omega_h^2}\text{Im}(C_M)\\ A_4^*(K_h)=\frac{1}{\rho B^3h_0\omega_h^2}\text{Re}(F_M)=\frac{U^2}{2Bh_0\omega_h^2}\text{Re}(C_M) 同理，使结构做扭转小振幅的稳态简谐运动，可以得到： H2∗(Kα)=1ρB3α0ωα2Im(FL)=U22B2α0ωα2Im(CL)H3∗(Kα)=1ρB3α0ωα2Re(FL)=U22B2α0ωα2Re(CL)A2∗(Kα)=1ρB4α0ωα2Im(FM)=U22B2α0ωα2Im(CM)A3∗(Kα)=1ρB4α0ωα2Re(FM)=U22B2α0ωα2Re(CM) H_2^*(K_\alpha)=\frac{1}{\rho B^3\alpha_0\omega_\alpha^2}\text{Im}(F_L)=\frac{U^2}{2B^2\alpha_0\omega_\alpha^2}\text{Im}(C_L)\\ H_3^*(K_\alpha)=\frac{1}{\rho B^3\alpha_0\omega_\alpha^2}\text{Re}(F_L)=\frac{U^2}{2B^2\alpha_0\omega_\alpha^2}\text{Re}(C_L)\\ A_2^*(K_\alpha)=\frac{1}{\rho B^4\alpha_0\omega_\alpha^2}\text{Im}(F_M)=\frac{U^2}{2B^2\alpha_0\omega_\alpha^2}\text{Im}(C_M)\\ A_3^*(K_\alpha)=\frac{1}{\rho B^4\alpha_0\omega_\alpha^2}\text{Re}(F_M)=\frac{U^2}{2B^2\alpha_0\omega_\alpha^2}\text{Re}(C_M) 因此可将识别三分力系数的频率组成以及其与对应位移的相位差的代码写入MATLAB函数文件中，返回值为对应的颤振导数值。以下代码为该功能的一种实现方法，可根据个人实际使用情况进行删除、修改和添加。AeroDerivatives.m代码如下：

function [reduced_U,D] = AeroDerivatives(Cp,time,freq,U,B,dsp_type,max_dsp,varargin)
%利用气动力求解颤振导数
%   Cp为气动力系数的时程
%   time为时间信号
%   freq表示考虑的特定频率
%   U为来流风速
%   B为特征尺度
%   dsp_type为位移类型,'tor'为扭转,'ver'为竖向位移
%   max_dsp为最大位移,扭转角以°为单位
%   varargin为fft中的窗函数,缺省时默认为矩形窗
%   输出D的顺序为[H1,H4]/[H2,H3];[A1,A4]/[A2,A3]
    %% 定义窗函数类型
    if nargin == 7
        wintype = 'rec';%默认为矩形窗
    elseif nargin == 8
        wintype = varargin{1};
    else
        disp('输入有误');
    end
    %% 三分力系数的傅里叶变换
    [fx,mag,phi]=fft1(Cp-mean(Cp),1/(time(2)-time(1)),wintype);%去除趋势项
    reduced_U=U/B./freq;%对应频率下的折算风速
    %% 力与位移的相位差计算
    D=zeros(1,2);%存储颤振导数值的空矩阵
    i=find(abs(fx-freq)/freq<0.05);
    Cp_mag=max(mag(i));i=find(mag==Cp_mag);
    Cp_fx=fx(i);Cp_phi=phi(i);%此段代码通过特定频率范围内最大幅值寻找到索引序号，从而得到辐角
    omega=2*pi*Cp_fx;

    dsp=sin(omega*time);%接下来对位移进行相位分析，构造的位移函数与UDF文件一致
    [fx,mag,phi]=fft1(dsp,1/(time(2)-time(1)),wintype);
    dsp_phi=floor(phi(find(mag==max(mag))));%位移的相位
    theta=(floor(Cp_phi)-dsp_phi)/180*pi;%气动力与位移的相位差
    %% 识别颤振导数值
    if dsp_type=='tor'
        alpha0=max_dsp/180*pi;
        D(1,1)=1/2*U^2*Cp_mag*sin(theta)/B^2/alpha0/omega^2;
        D(1,2)=1/2*U^2*Cp_mag*cos(theta)/B^2/alpha0/omega^2;
    elseif dsp_type=='ver'
        h0=max_dsp;
        D(1,1)=1/2*U^2*Cp_mag*sin(theta)/B/h0/omega^2;
        D(1,2)=1/2*U^2*Cp_mag*cos(theta)/B/h0/omega^2;
    else
        disp('ERROR:位移类型输入错误');
    end
end

在MATLAB的脚本文件中编写利用采集的三分力系数数据和上述函数识别颤振导数的代码。具体实现如下：

clc
clear
format short
%% Parameter Settings
Clfolder='D:\cl_f1.out';
Cmfolder='D:\cm_f1.out';
U=3.5;B=0.833;%算例设置的参数
rU=[8];f=U/B./rU;%结构振动频率
data_length=1904*2;%数据长度，采用整周期采样，减少泄漏
motiontype='ver';%或'tor'
motionmag=0.004;%或1
window='han';%窗函数类型
%% The following code can remain the same
%% Input file
delimiterIn  = ' '; % 字符分隔符
headerlinesIn = 4;   % 文件头的行数
Climdata = importdata(Clfolder, delimiterIn, headerlinesIn);
Climdata = Climdata.data;
Cmimdata = importdata(Cmfolder, delimiterIn, headerlinesIn);
Cmimdata = Cmimdata.data;
%% Initialize empty vector
H=zeros(length(f),2);
A=zeros(length(f),2);
%% Calculate aeroderivatives
for i=1:length(f)
    time=Climdata(end-data_length+1:end,2);%时间
    Cl=Climdata(end-data_length+1:end,3);%升力系数
    Cm=Cmimdata(end-data_length+1:end,3);%升力矩系数

    [UU,HH]=AeroDerivatives(Cl-mean(Cl),time,f(i),U,B,motiontype,motionmag,window);%气动力零均值化
    H(i,1:2)=HH;
    [UU,AA]=AeroDerivatives(Cm-mean(Cm),time,f(i),U,B,motiontype,motionmag,window);%气动力零均值化
    A(i,1:2)=AA;
end
%% Disp
disp('H=');disp(H);
disp('A=');disp(A);

上述代码输出的结果如下：

[H1,H2,H3,H4]=
   -2.2177    -0.9775    -3.0085    0.391
[A1,A2,A3,A4]=
    0.6438    -0.2454    0.8557    0.1135
  1. 时域方法

相比于频域方法，时域方法没有对采样时间等参数有更多的要求。颤振导数的识别方法在代码层面更易实现。实际上时域方法的颤振导数识别即为一种非线性拟合方法。以下的代码采用MATLAB中的nlinfit函数拟合颤振导数。具体可参考MATLAB支持文档：非线性回归 - MATLAB nlinfit - MathWorks 中国

注：下述代码可以带着警告运行。当只识别与竖向振动有关的颤振导数时，其他颤振导数值保持初始值不会改变。反之亦然。

clc
clear
format short
%% Parameter Settings
data_length=3800;%数据长度，可以不是整数周期
Clfolder='D:\cl_f1.out';
Cmfolder='D:\cm_f1.out';
a=[0.1,0.1,0.1,0.1];%迭代最小二乘估计方法的初始值
X=zeros(size(Cl,1),4);%存放运动特征值的向量
h0=0.004;alpha0=1/180*pi;
B=0.833;U=3.5;
fa=0.525210084;%或为0
fh=0;%或为0.525210084
%% The following code can remain the same
%% Input file
delimiterIn  = ' '; % 字符分隔符
headerlinesIn = 4;   % 文件头的行数
Climdata = importdata(Clfolder, delimiterIn, headerlinesIn);
Climdata = Climdata.data;
Cmimdata = importdata(Cmfolder, delimiterIn, headerlinesIn);
Cmimdata = Cmimdata.data;
time=Climdata(end-data_length+1:end,2);%时间
Cl=Climdata(end-data_length+1:end,3);%升力系数
Cm=Cmimdata(end-data_length+1:end,3);%升力矩系数

%% Reduced Frequency
Kh=2*pi*fh*B/U;
Ka=2*pi*fa*B/U;

%% Initialize motion vectors
X(:,1)=h0*2.0*pi*fh*cos(2.0*pi*fh*time);
X(:,2)=alpha0*2.0*pi*fa*cos(2.0*pi*fa*time);
X(:,3)=alpha0*sin(2.0*pi*fa*time);
X(:,4)=h0*sin(2.0*pi*fh*time);

%% Calculate aeroderivatives
N=[2*Kh/U,0,0,0;0,2*B*Ka/U,0,0;0,0,2*Ka^2,0;0,0,0,2*Kh^2/B];%Scanlan自激力模型中的系数
A=nlinfit(X,Cm-mean(Cm),(a,X)(X*(N'*a')),a);
H=nlinfit(X,Cl-mean(Cl),(a,X)(X*(N'*a')),a);
%% Disp
disp('H=');disp(H);
disp('A=');disp(A);

上述代码输出的结果如下：

[H1,H2,H3,H4]=
   -2.2237    -0.9492    -3.0205    0.3587
[A1,A2,A3,A4]=
    0.6436    -0.2487    0.8554    0.1162

值得指出的是，时域方法相比于频域方法对参数的要求更少，但是一些参数如采样时间的改变仍然会影响到颤振导数的识别。

  1. 频域方法和时域方法的比较

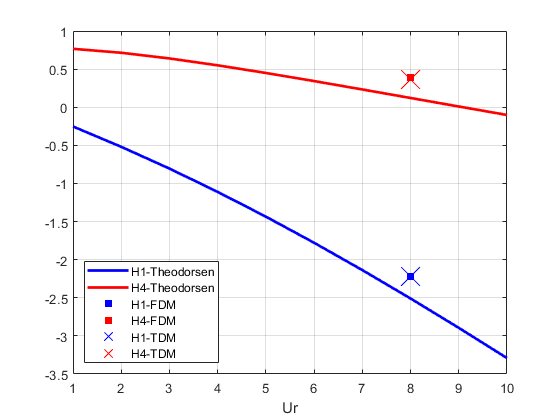
简单地对该案例在折算风速为8时采用两种识别方法计算的颤振导数值进行比较。 如下表和下图所示：

频域识别方法 时域识别方法 Theodorsen理论解 两者相对误差（以时域方法为参考）/%
H1∗H_1^* -2.2177 -2.2237 -2.5095 0.30
H2∗H_2^* -0.9775 -0.9492 -0.7817 -3.00
H3∗H_3^* -3.0085 -3.0205 -3.3613 0.40
H4∗H_4^* 0.3910 0.3587 0.1212 9.00
A1∗A_1^* 0.6438 0.6436 0.6274 0.10
A2∗A_2^* -0.2454 -0.2487 -0.3046 1.30
A3∗A_3^* 0.8557 0.8554 0.8649 0.10
A4∗A_4^* 0.1135 0.1162 0.1661 -2.30

FDMTDM-1FDMTDM-2

FDMTDM-3FDMTDM-4

注：图中FDM为频域识别方法（Frequency Domain Method）,TDM为时域识别方法（Time Domain Method）,

由以上的结果可以看到，除去单个颤振导数值（H4∗H_4^*）的识别频域方法和时域方法有9%的误差外，其余颤振导数值两者识别结果一致。即，

从识别的结果上看，频域和时域两类识别方法并无高下之分。但是由于频域方法需要考虑非整数周期采样导致的信号泄漏问题，在数据采集和参数识别上需要更精确的操作。所以时域方法是分状态单频强迫振动法识别颤振导数的推荐方法。

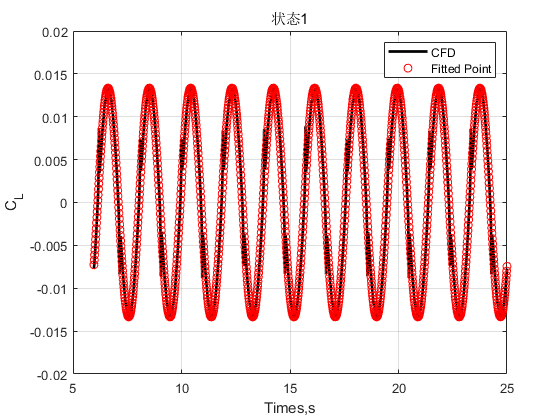
最后，绘制状态1CFD采集气动力系数数据与时域方法拟合曲线（CFD采集气动力系数数据已经减去平均值）的比较，以证明采集数据的尖刺点不影响颤振导数的识别。

Fitted-1Fitted-2

至此，MATLAB处理气动力数据的操作介绍完成。

results matching ""

    No results matching ""