第八节 提高计算速度（实现篇）

本文以薄平板为结构案例，实现不同方法识别同一断面在不同折算风速下的颤振导数。

本文中采取的案例如下：

B（桥面宽） H（高） 风嘴形状 i（桥面横坡） 缩尺比 U风速 Re雷诺数
50 0.5 圆弧 0 1：50 2.9 2E5

注：表中长度单位为m，速度单位为m/s

Section

折算风速定为4和8，对应强迫振动频率为0.7250Hz和0.3625Hz。

1、分状态单频强迫振动法

理想薄平板的颤振导数存在Theodorsen理论解。本节考虑分状态单频强迫振动法作为基础的识别颤振导数方法，其识别结果应先与Theodorsen理论解进行比较。之后可将分状态单频强迫振动法的识别结果作为参考值，其他方法计算出的颤振导数值与其进行比较。

本节先通过UDF文件+FLUENT先计算出该断面在不同折算风速下的自激力。两种折算风速需要完成4次计算。（出于简单考虑，该自激力未扣除零风速下的动态力）再通过自激力采用时域方法识别出不同折算风速下的8个颤振导数值。结构的强迫振动如下给出： h=0.001×sin(2πft),α=0α=π/180×sin(2πft),h=0f=0.7250Hz,0.3625Hz(1) h=0.001\times sin(2\pi ft),\alpha=0\\ \alpha=\pi/180\times sin(2\pi ft),h=0\\ f=0.7250Hz,0.3625Hz\\ \tag{1} 计算结果如下表所示：

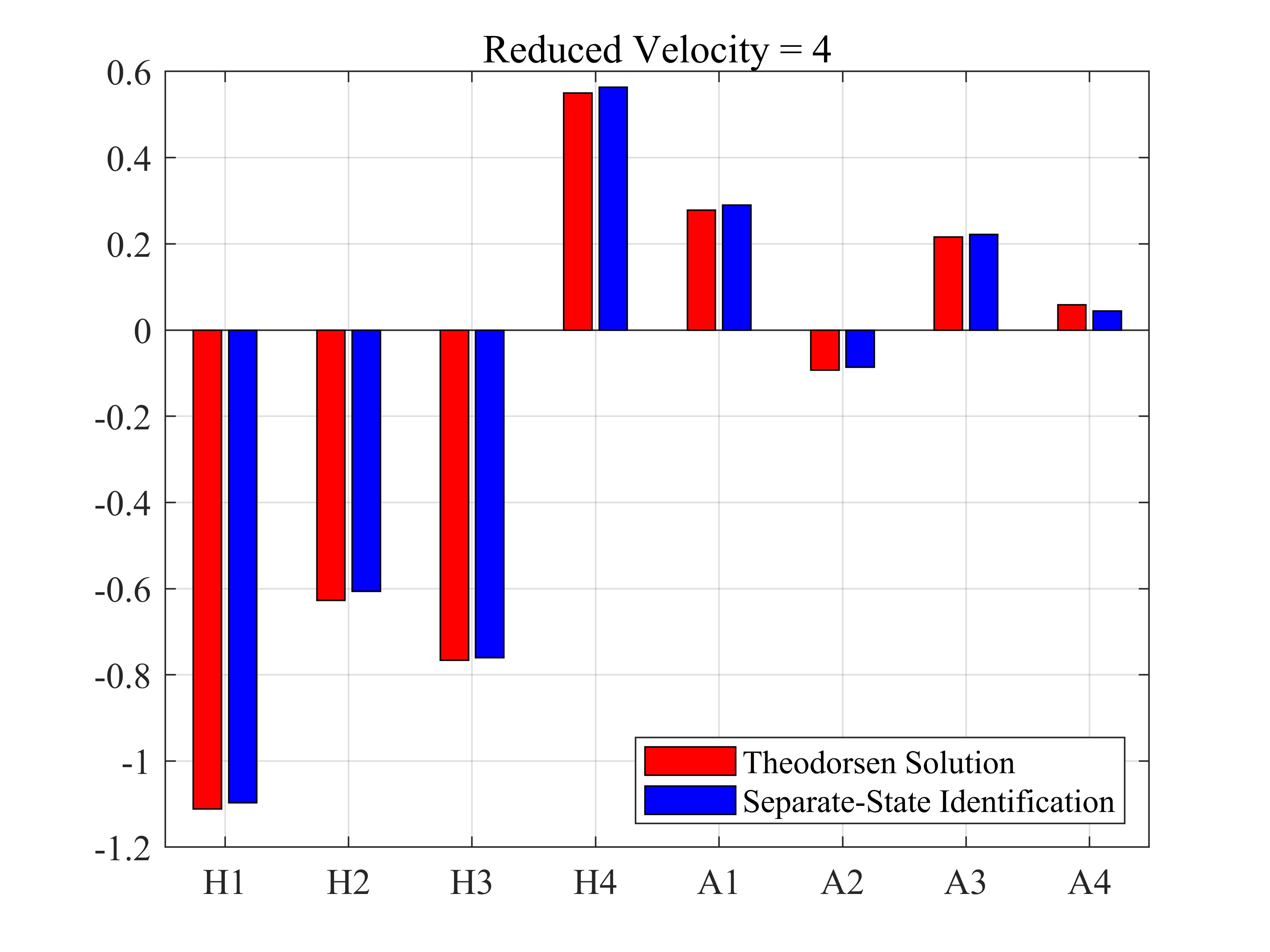
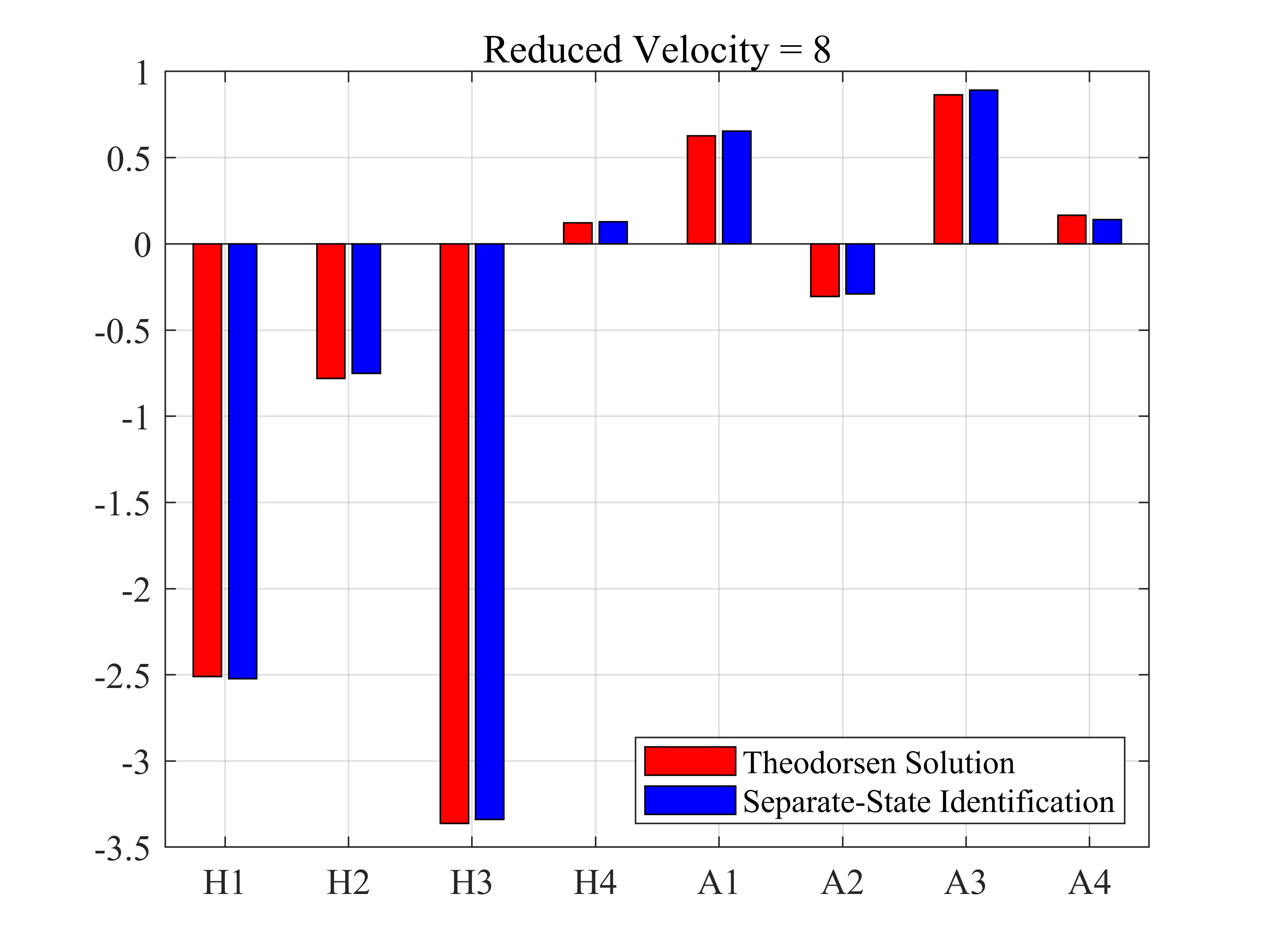
表1 Theodorsen理论解

UrU_r H1∗H_1^* H2∗H_2^* H3∗H_3^* H4∗H_4^* A1∗A_1^* A2∗A_2^* A3∗A_3^* A4∗A_4^*
4 -1.1111 -0.6277 -0.7663 0.5497 0.2778 -0.0931 0.2161 0.0589
8 -2.5095 -0.7817 -3.3613 0.1212 0.6274 -0.3046 0.8649 0.1661

表2 分状态单频强迫振动法时域识别结果

UrU_r H1∗H_1^* H2∗H_2^* H3∗H_3^* H4∗H_4^* A1∗A_1^* A2∗A_2^* A3∗A_3^* A4∗A_4^*
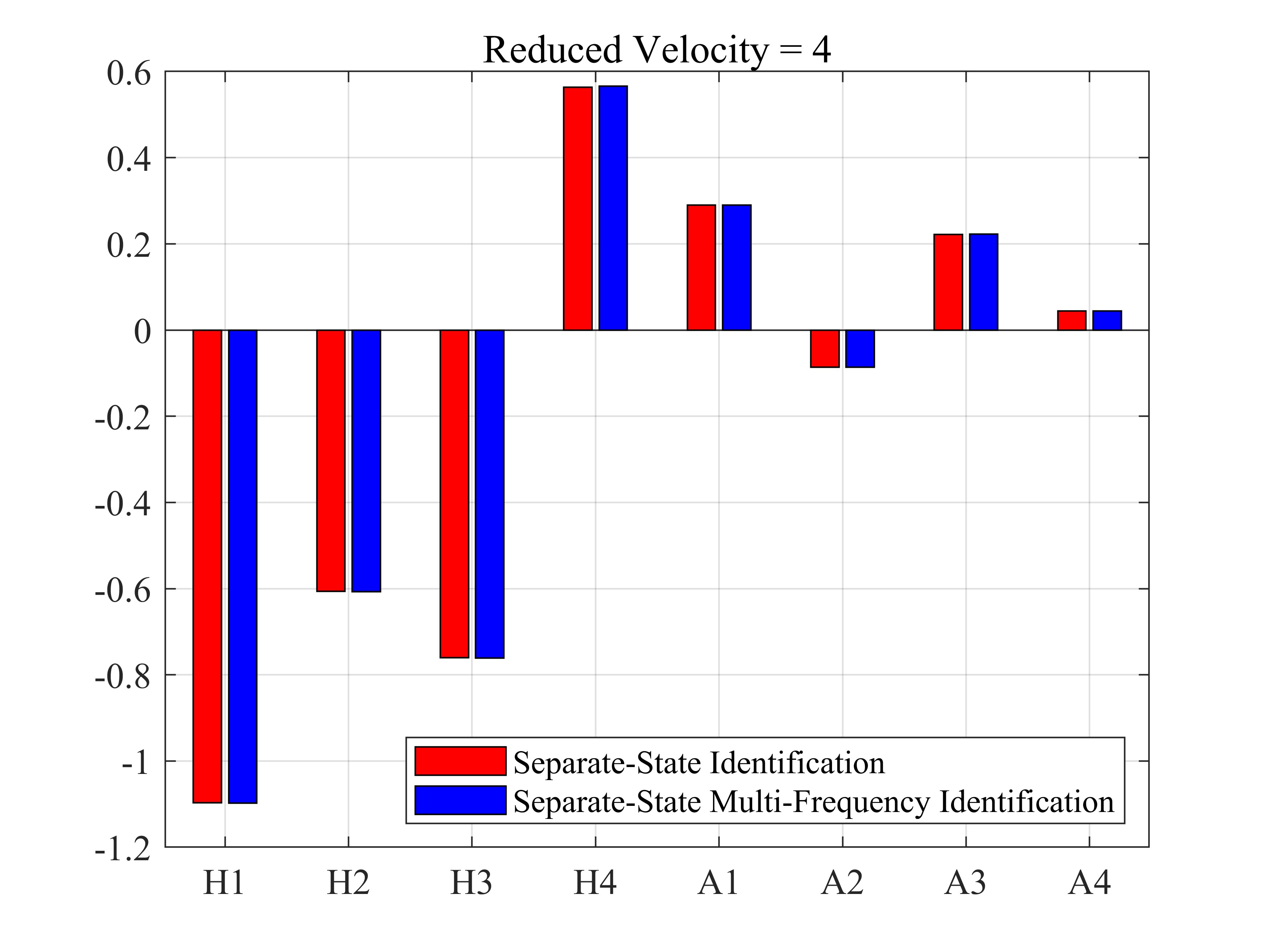
4 -1.0969 -0.6062 -0.7599 0.5636 0.2899 -0.0866 0.2217 0.0441
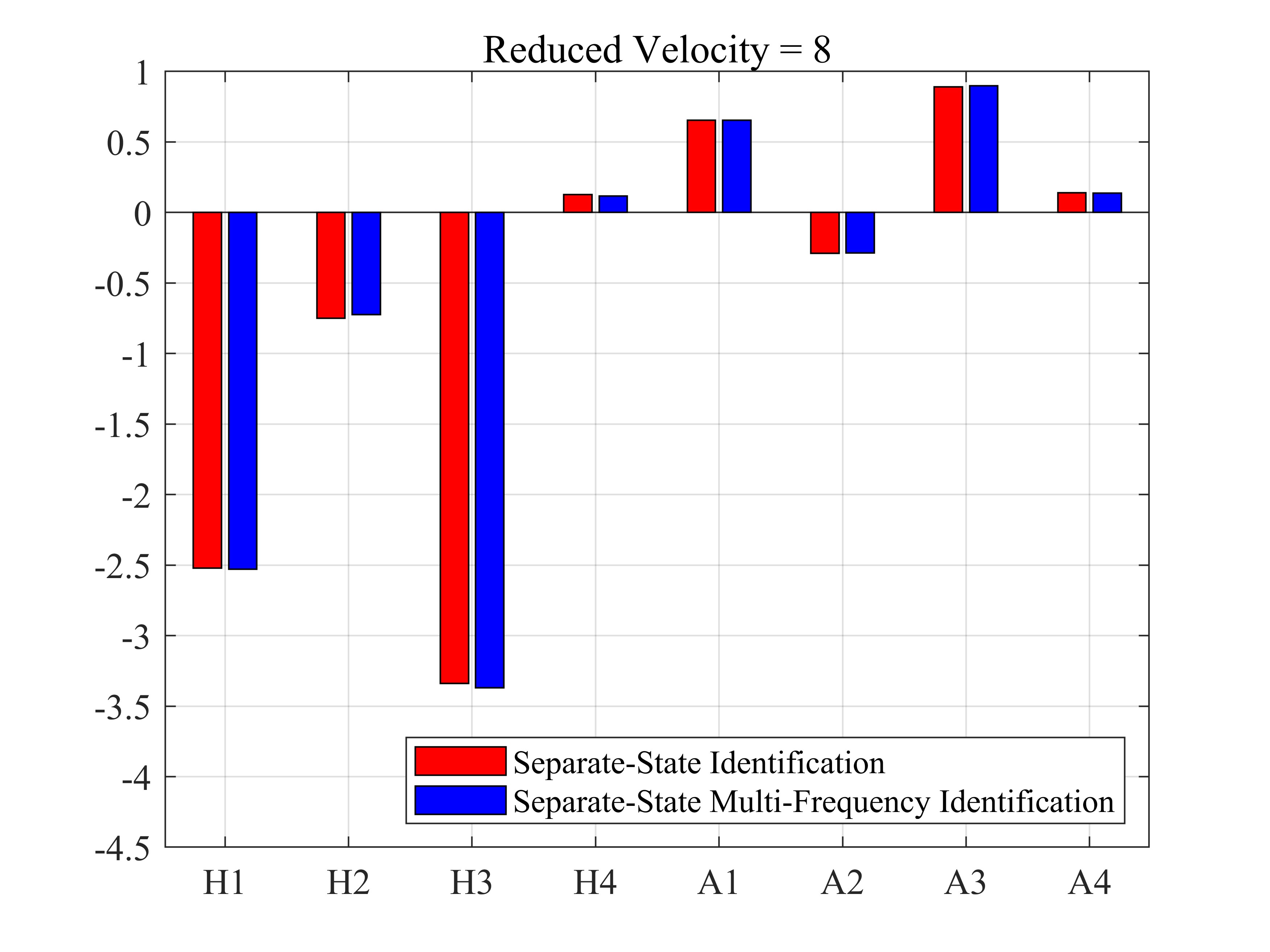
8 -2.5224 -0.7510 -3.3393 0.1278 0.6532 -0.2905 0.8920 0.1404

表3 时域识别结果与理论解误差（以理论解为基准）

UrU_r H1∗H_1^* H2∗H_2^* H3∗H_3^* H4∗H_4^* A1∗A_1^* A2∗A_2^* A3∗A_3^* A4∗A_4^*
4 1.3% 3.4% 0.8% 2.5% 4.3% 7.0% 2.6% -25.1%
8 -0.5% 3.9% 0.7% 5.5% 4.1% 4.6% 3.1% -15.4%

Separated State Single Freq U=4

Separated State Single Freq U=8

由上数据可知，两种折算风速下，分状态单频强迫振动识别结果与Theodorsen理论解除了$A_4^*$外其他颤振导数基本一致。该结果与部分大于5%的误差，不排除是非理想薄平板引起的。

2、耦合状态强迫振动法

耦合状态强迫振动法需要断面做竖弯与扭转耦合的强迫振动，且两者振动频率不应相同。两种折算风速需要完成2次计算。

本节通过UDF文件+FLUENT先计算出该断面在不同耦合状态下的自激力。（出于简单考虑，该自激力未扣除零风速下的动态力）再通过自激力采用时域方法识别出不同折算风速下的8个颤振导数值。结构的强迫振动如下给出：

h=0.001×sin(2πf1t),α=π/180×sin(2πf2t)h=0.001×sin(2πf2t),α=π/180×sin(2πf1t)f1=0.7250Hz,f2=0.3625Hz(2) h=0.001\times sin(2\pi f_1t),\alpha=\pi/180\times sin(2\pi f_2t)\\ h=0.001\times sin(2\pi f_2t),\alpha=\pi/180\times sin(2\pi f_1t)\\ f_1=0.7250Hz,f_2=0.3625Hz\\ \tag{2} 计算结果如下表所示：计算结果如下表所示：

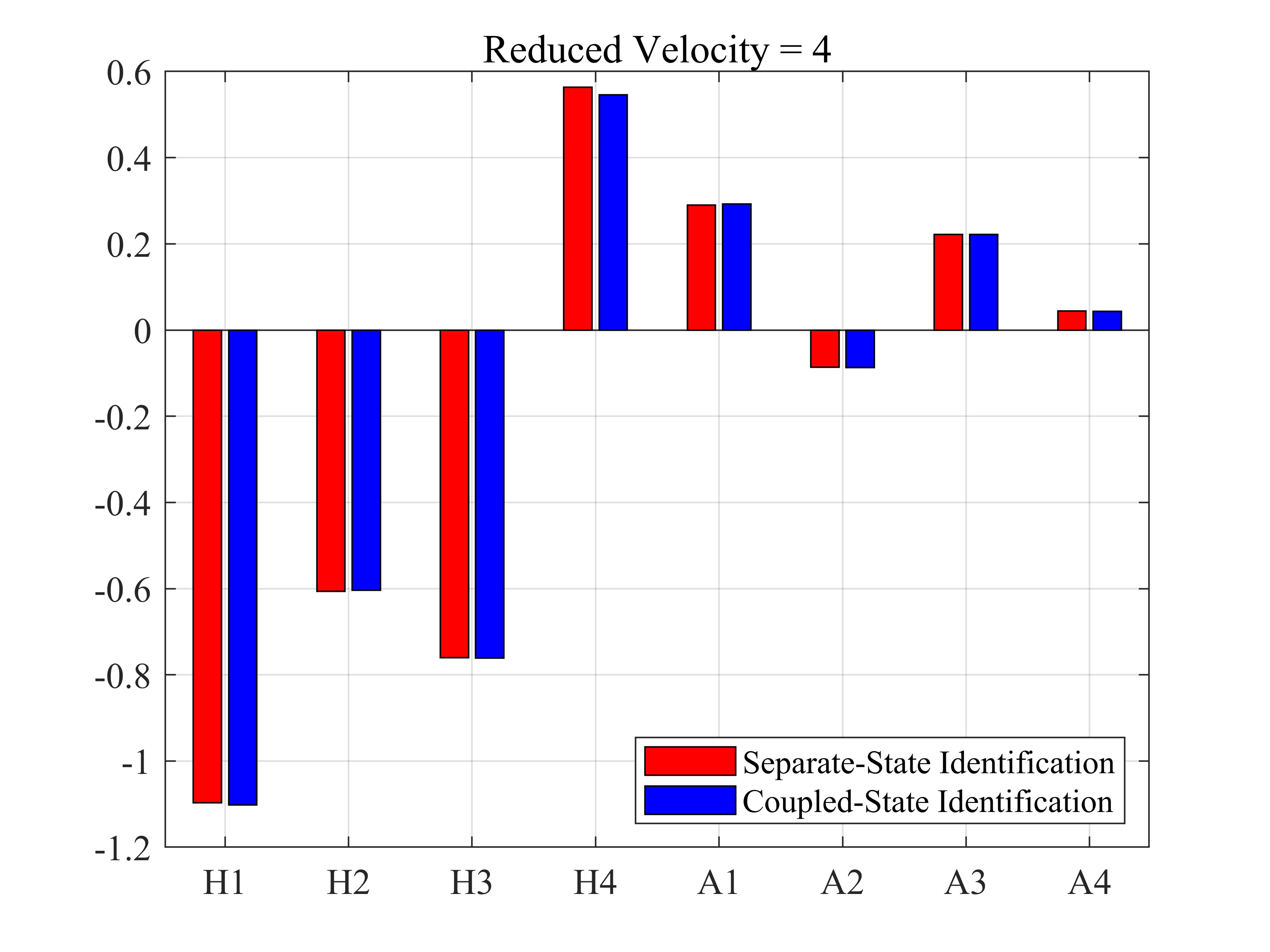
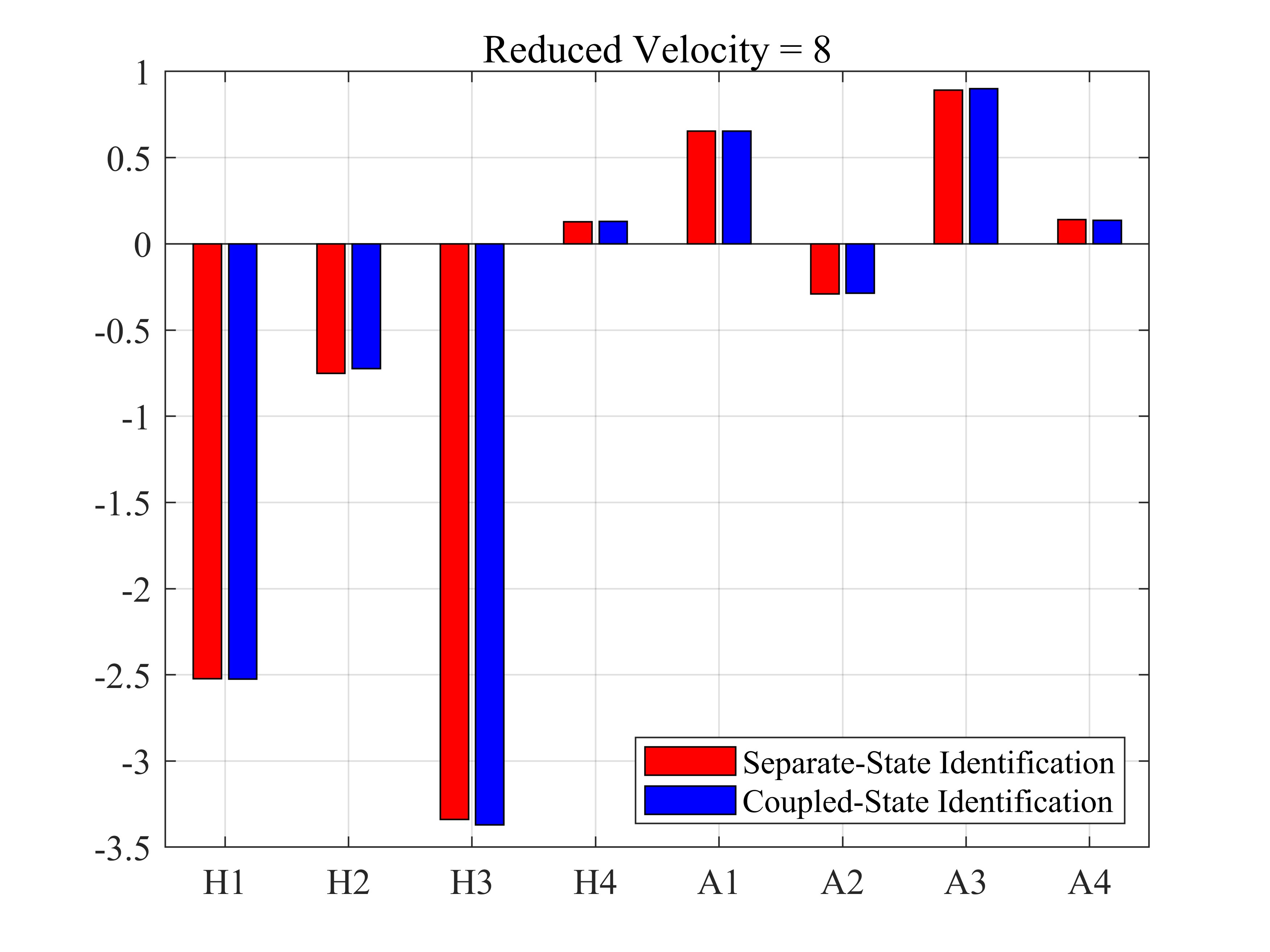
表4 耦合状态强迫振动法时域识别结果

UrU_r H1∗H_1^* H2∗H_2^* H3∗H_3^* H4∗H_4^* A1∗A_1^* A2∗A_2^* A3∗A_3^* A4∗A_4^*
4 -1.1016 -0.6035 -0.7608 0.5458 0.2925 -0.0867 0.2221 0.0432
8 -2.5255 -0.7238 -3.3709 0.1296 0.6547 -0.2862 0.8992 0.1363

表5 耦合状态强迫振动法识别结果与分状态单频强迫振动法识别结果误差（以分状态单频强迫振动法为基准）

UrU_r H1∗H_1^* H2∗H_2^* H3∗H_3^* H4∗H_4^* A1∗A_1^* A2∗A_2^* A3∗A_3^* A4∗A_4^*
4 -0.4% 0.4% -0.1% -3.2% 0.9% -0.2% 0.2% -2.1%
8 -0.1% 3.6% -0.9% 1.4% 0.2% 1.5% 0.8% -3.0%

Coupled State Forced Vibration U=4

Coupled State Forced Vibration U=8

由上数据可知，两种折算风速下，耦合状态强迫振动识别结果与分状态单频强迫振动识别结果基本一致。因此在小振幅运动下，可以通过耦合状态强迫振动方法减少计算量而不失计算精度。

3、分状态多频强迫振动法

分状态多频强迫振动法需要断面分别做竖弯与扭转的强迫振动。每种运动含有多种频率。两种折算风速需要完成2次计算。

本节通过UDF文件+FLUENT先计算出该断面在不同运动状态下的自激力。（出于简单考虑，该自激力未扣除零风速下的动态力）再通过自激力采用时域方法识别出不同折算风速下的8个颤振导数值。结构的强迫振动如下给出：

h=0.001×sin(2πf1t)+0.001×sin(2πf2t)α=π/180×sin(2πf1t)+π/180×sin(2πf2t)f1=0.7250Hz,f2=0.3625Hz(3) h=0.001\times sin(2\pi f_1t)+0.001\times sin(2\pi f_2t)\\ \alpha=\pi/180\times sin(2\pi f_1t)+\pi/180\times sin(2\pi f_2t)\\ f_1=0.7250Hz,f_2=0.3625Hz\\ \tag{3} 计算结果如下表所示：计算结果如下表所示：

表6 分状态多频强迫振动法时域识别结果

UrU_r H1∗H_1^* H2∗H_2^* H3∗H_3^* H4∗H_4^* A1∗A_1^* A2∗A_2^* A3∗A_3^* A4∗A_4^*
4 -1.0978 -0.6068 -0.7608 0.5656 0.2897 -0.0863 0.2222 0.0441
8 -2.5283 -0.7230 -3.3697 0.1157 0.6542 -0.2871 0.8976 0.1386

表7 分状态多频强迫振动法识别结果与分状态单频强迫振动法识别结果误差（以分状态单频强迫振动法为基准）

UrU_r H1∗H_1^* H2∗H_2^* H3∗H_3^* H4∗H_4^* A1∗A_1^* A2∗A_2^* A3∗A_3^* A4∗A_4^*
4 -0.1% -0.1% -0.1% 0.4% -0.1% 0.3% 0.2% -0.1%
8 -0.2% 3.7% -0.9% -9.4% 0.2% 1.2% 0.6% -1.3%

Separated State Multi-Freq U=4

Separated State Multi-Freq U=8

由上数据可知，两种折算风速下，分状态多频强迫振动识别结果与分状态单频强迫振动识别结果除了在折算频率为8时的H4∗H_4^*误差超过5%外，其他结果基本一致。该误差可能是该案例计算的时间总长过小导致的识别误差。不失一般性地可以认为，在小振幅运动下，可通过分状态多频强迫振动方法减少计算量而不失计算精度。

4、总结

本章通过三种颤振导数识别方法——分状态单频强迫振动、耦合状态强迫振动和分状态多频强迫振动方法，对薄平板结构进行了两种折算频率下的颤振导数的识别。基本结论如下：

  1. 分状态单频强迫振动识别结果与Theodosen理论解接近（除了A4∗A_4^*），可以作为其他方法的参考识别结果。
  2. 在小振幅运动给定下，三种识别方法的结果基本一致。
  3. 尽管案例两种折算风速存在倍数关系，但是通过识别结果可以看出，在小振幅运动下，气动力倍频现象未影响到颤振导数的识别。
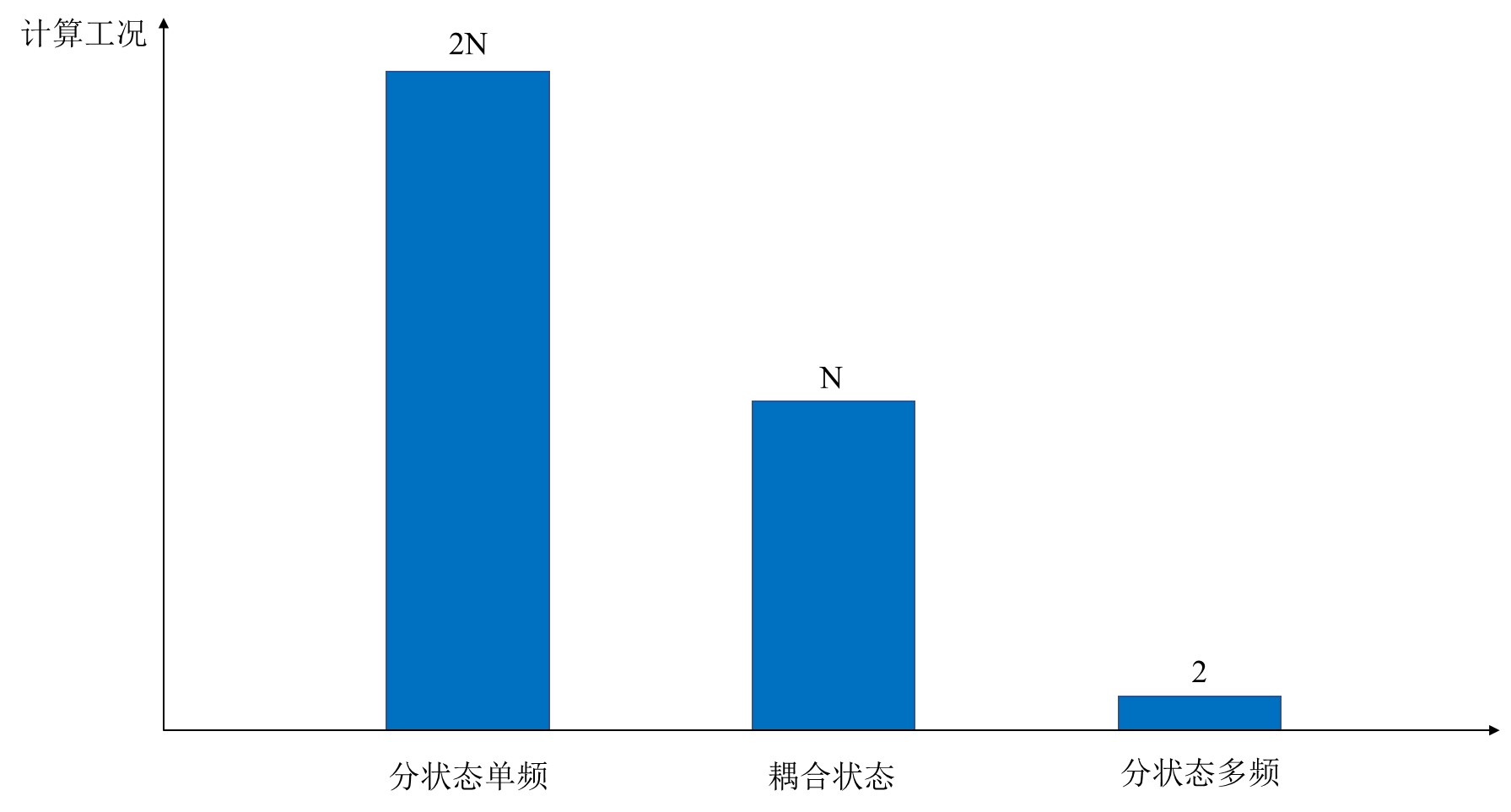
  4. 分状态单频强迫振动方法识别结果可靠，但是计算量大。对于N个折算风速，总共需要计算2N个工况才能确定主要的8种颤振导数。而耦合状态强迫振动方法只需要N个工况。分状态多频强迫振动方法所需工况最少，仅需要2个工况。但是后两种方法要求强迫运动振幅够小以满足线性叠加理论，并且能规避气动力倍频带来的影响。一般而言，竖向运动振幅宜小于D/200，D为特征尺寸，扭转运动振幅宜小于2°。

Compare

results matching ""

    No results matching ""