MATLAB常用滤波器设计

1、分贝

分贝是量度两个相同单位之数量比例的计量单位，主要用于度量声音强度，常用dB表示。可表示为：

1. 表示功率量之比的一种单位，等于功率强度之比的常用对数的10倍。
2. 表示场量之比的一种单位，等于场强幅值之比的常用对数的20倍。

$$功率类：10lg(P_{out}/P_{in})\\ 场量类：20lg(V_{out}/V_{in}) \tag{1}$$

因为传导发射（如电压、电流等）和辐射发射（电场、磁场等）的量取值范围相当大，在应用中非常不方便描述。所以使用分贝可以压缩数据，将较大的数量压缩成较小的数量。

2、经典滤波器概念

数字滤波器是指输入、输出均为数字信号，通过数值运算处理改变输入信号所含频率成分的相对比例，或者滤除某些频率成分的数字器件或程序。经典滤波器是是数字滤波器的一种。

经典滤波器特点时输入信号中有用的频率成分和希望滤除的频率成分各占有不同的频带，通过一个合适的选频滤波器滤除干扰，得到纯净信号，达到滤波的目的。

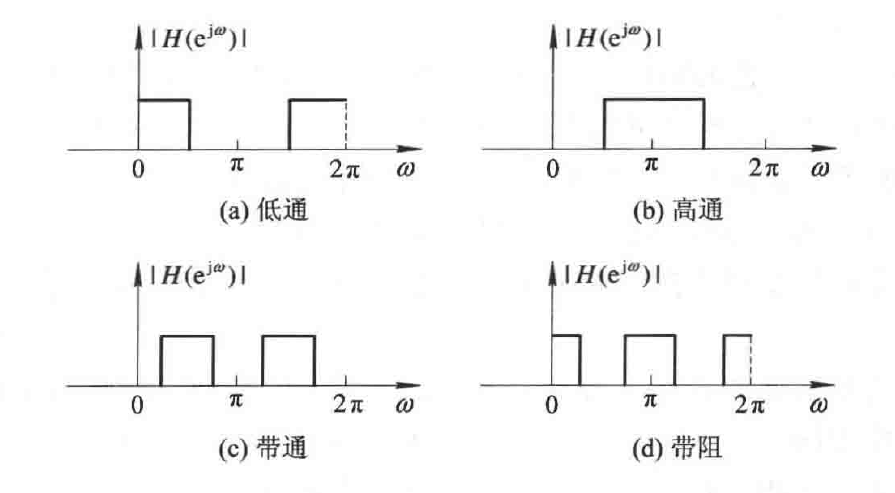
经典数字滤波器从滤波特性上分类，可以分成低通、高通、带通和带阻等滤波器。他们的理想幅频特性如图所示。这种理想滤波器是不可能实现的，我们只能按照某些准则设计滤波器，使之在误差容限内逼近理想滤波器。

数字滤波器可以理解为构造一种频响函数，完成在频域内滤波的目的。其频率响应函数$H(e^{j\omega})$都是以$2\pi$为周期的。一般在数字频率的主值区$[-\pi,\pi]$描述数字滤波器的频率响应特性。

3、经典滤波器的技术指标

假设数字滤波器的频率响应函数$H(e^{jw})$用下式表示： $$H(e^{jw})=|H(e^{jw})|e^{j\theta(\omega)} \tag{2}$$ 式中，$|H(e^{jw})|$称为幅频特性函数；$\theta(\omega)$称为相频特性函数。前者表示信号通过该滤波器后各频率成分振幅衰减情况；后者表示各频率成分通过滤波器后在时间上的延时情况。即使两个滤波器幅频特性相同，相频特性不同，对相同的输入，滤波器输出的信号波形也是不一样的。一般选频滤波器的技术指标由幅频特性给出，对几种典型滤波器（如巴特沃斯滤波器），其相频特性是确定的。所以设计过程中，相频特性一般不做要求。

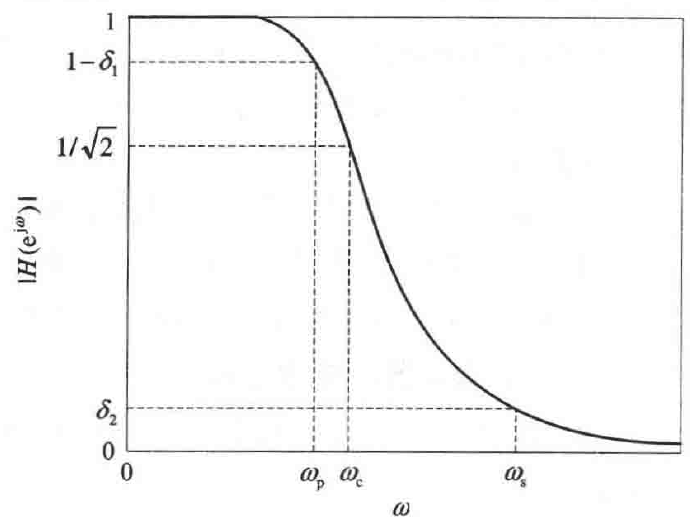
下面以低通滤波器为例，介绍经典滤波器的技术指标。由于是理想滤波器的近似实现，因此通带不是完全水平的，阻带不是绝对衰减到零，且在通带与阻带之间设置一定宽度的过渡带。下图表示低通滤波器的幅频特性。

$\omega_p$和$\omega_s$分别称为通带边界频率和阻带截止频率。通带频率范围为$0\leq\omega\leq\omega_p$，在通带中要求$(1-\delta_1)\lt|H(e^{jw})|\leq1$，阻带频率范围为$\omega_s\leq|\omega|\leq\pi$，在阻带要求$|H(e^{j\omega})|\leq\delta_2$。从$\omega_p$到$\omega_s$称为过渡带，过渡带上的频响一般是单调下降的。通常，通带内和阻带内允许的衰减一般用分贝数表示，通带内允许的最大衰减$\alpha_p$表示，阻带内允许的最小衰减用$\alpha_s$表示。对低通滤波器，$\alpha_p$和$\alpha_s$分别定义为： $$\alpha_p=20lg\frac {max|H(e^{jw})|}{min|H(e^{jw})|}\quad dB\\ \alpha_s=20lg\frac {通带中max|H(e^{jw})|}{阻带中min|H(e^{jw})|}\quad dB\\ \tag{3}$$ 低通滤波器的设计指标完全由通带边界频率$\omega_p$、通带最大衰减$\alpha_p$、阻带边界频率$\omega_s$和阻带最小衰减$\alpha_s$确定。

如果将$|H(e^{j0})|$归一化为1，则 $$\alpha_p=-20lg{H(e^{j\omega_p})}\quad dB\\ \alpha_s=-20lg{H(e^{j\omega_s})}\quad dB\\ \tag{4}$$ 当幅度下降到$\sqrt(2)/2$时，标记$\omega=\omega_c$，此时$\alpha=-20lg|H(j\omega_c)|=3\quad dB$，称$\omega_c$为3dB通带截止频率。$\omega_p$、$\omega_c$和$\omega_s$称为边界频率，这些是滤波器设计中所设计到的重要参数。

3、模拟低通滤波器设计指标以及逼近方法

选频型模拟滤波器按幅频特性可分成低通、高通、带通和带阻滤波器。设计时一般是先设计低通滤波器，再通过频率变换将低通滤波器转换成希望类型的滤波器。因此在介绍理论方法时，以低通滤波器为主。

设计模拟滤波器时，设计指标一般由幅频响应函数$|H(j\omega)|$（或$|H(j\Omega)|$）给出。一般实际使用损耗函数（或是衰减函数）$A(\Omega)$来描述滤波器的幅频响应特性。对归一化幅频响应函数（$max|H(j\Omega)=1|$），$A(\Omega)$定义如下： $$A(\Omega)=-20lg|H(j\Omega)|=-10|H(j\Omega)|^2\quad dB \tag{5}$$ 损耗函数的优点是对幅频响应的取值非线性压缩，放大了小的幅度，从而可以同时观察通带和阻带频响特性的变化情况。

另外，由于直接画出损耗函数曲线图正好与幅频特性曲线形状相反，所以习惯将$-A(\Omega)$曲线称为损耗函数。

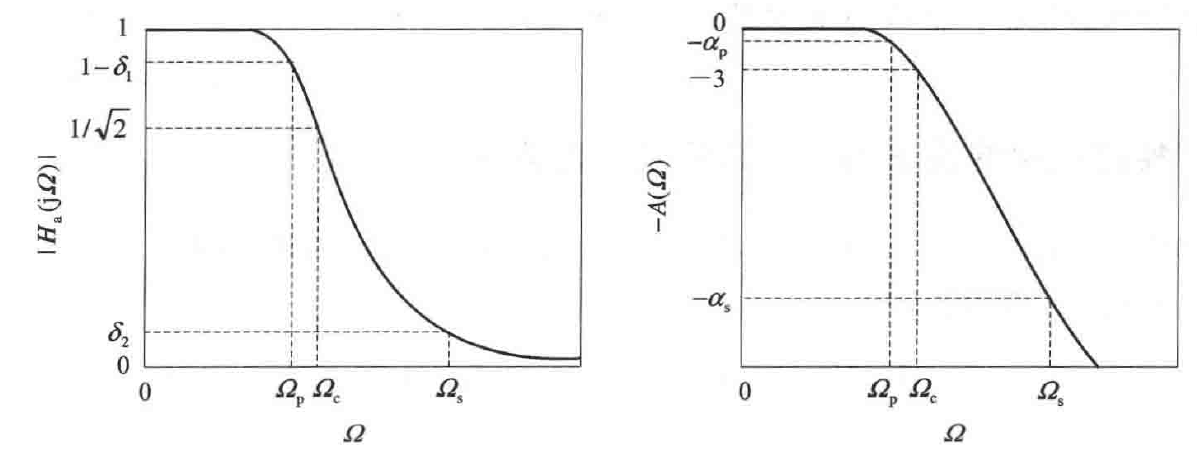
模拟低通滤波器的设计指标参数有$\alpha_p$、$\Omega_p$、$\alpha_s$和$\Omega_s$。其中$\Omega_p$和$\Omega_s$分别称为通带边界频率和阻带截止频率。$\alpha_p$称为通带最大衰减，$\alpha_s$称为阻带最小衰减。$\alpha_p$和$\alpha_s$的单位为dB。下图左图为幅频特性描述，右图为损耗函数描述。

4、典型低通滤波器特点

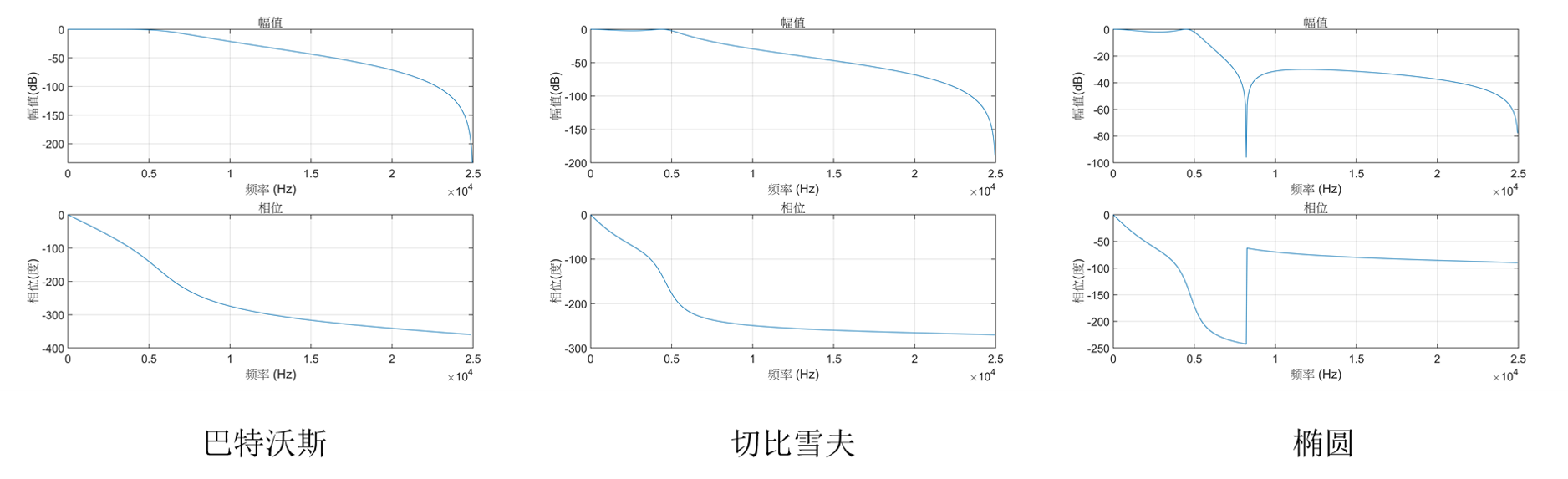
有三种典型的模拟滤波器：巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。巴特沃斯滤波器具有i单调下降的幅频特性；切比雪夫滤波器在通带或阻带内有等波纹特性；椭圆滤波器选择性相比前两者时最好的。

1、巴特沃斯低通滤波器

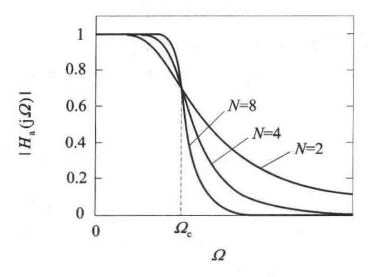
巴特沃斯低通滤波器的幅度平方函数$|H(j\Omega)|^2$用下式表示： $$|H(j\Omega)|^2=\frac{1}{1+(\frac{\Omega}{\Omega_c})^{2N}}$$ 式中，N称为滤波器的阶数。幅度下降的速度与阶数N有关，N愈大，通带愈平坦，过渡带愈窄，过渡带与阻带幅度下降的速度愈快，总的频响特性与理想低通滤波器的误差愈小。

2、切比雪夫低通滤波器

不同于单调下降的巴特沃斯低通滤波器，更有效的设计方法是将逼近精确度均匀地分布在整个通带内，或者均匀分布在整个阻带内，或者同时均匀分布在两者之内。这样可以使滤波器阶数大大降低。

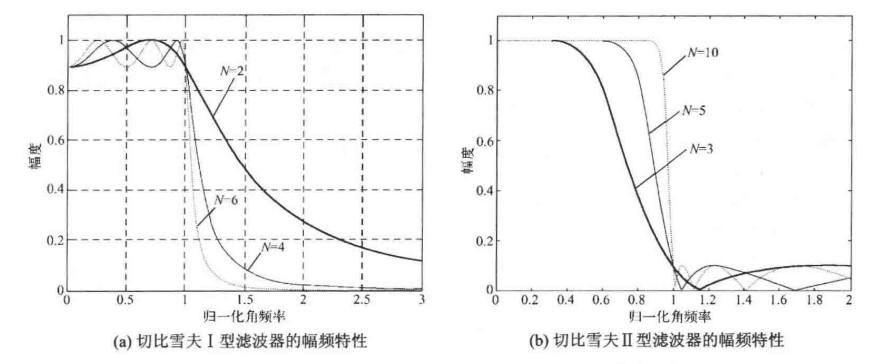
切比雪夫滤波器的幅频特性具有这种等波纹特性。它有两种形式：幅频特性在通带内是等波纹的、在阻带内是单调下降的切比雪夫Ⅰ型滤波器；幅频特性在通带内是单调下降、在阻带内是等波纹的切比雪夫Ⅱ滤波器。

这里介绍切比雪夫Ⅰ型滤波器的设计幅度平方函数$|H(j\Omega)|^2$： $$|H(j\Omega)|^2=\frac{1}{1+\epsilon^2C_N^2(\frac{\Omega}{\Omega_p})}$$ 式中，$\epsilon$为小于1的正数，表示通带内幅度波动的程度，$\epsilon$越大，波动幅度也越大；$\Omega_p$称为通带截止频率。

$C_N(x)$称为N阶切比雪夫多项式，定义如下： $$C_N(x)=\begin{cases} cos(Narccosx)\quad|x|\leq1\\ ch(Narchx)\quad\quad|x|\geq1\\ \end{cases}$$ 阶数N影响过渡带的宽度，同时也影响通带内波动的疏密，因为N等于通带内最大值与最小值的总个数。

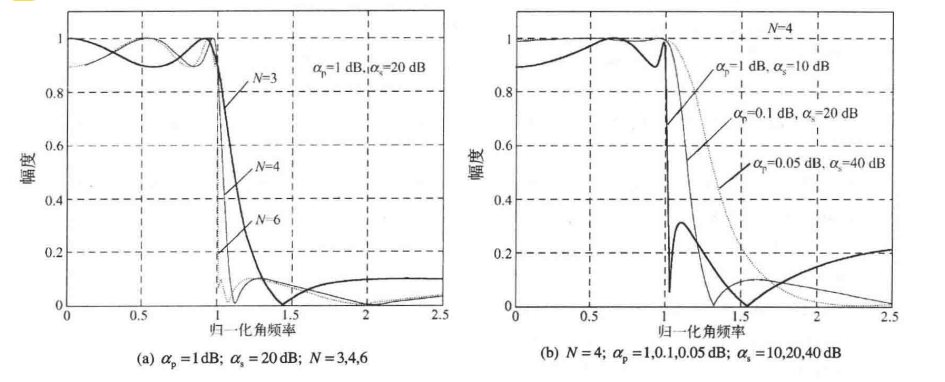
3、椭圆低通滤波器

椭圆滤波器在通带和阻带内都具有等波纹幅频响应特性。党旗通带和阻带波纹幅度固定时，阶数越高，过渡带越窄；当其阶数固定时，通带和阻带波纹幅度越小，过渡带就越宽。当阶数相同时，椭圆滤波器可以获得对理想滤波器幅频响应的最好逼近。

椭圆滤波器逼近理论是复杂的纯数学问题，详细推导不作介绍。

5、频率变换与模拟高通、带通、带阻滤波器的设计

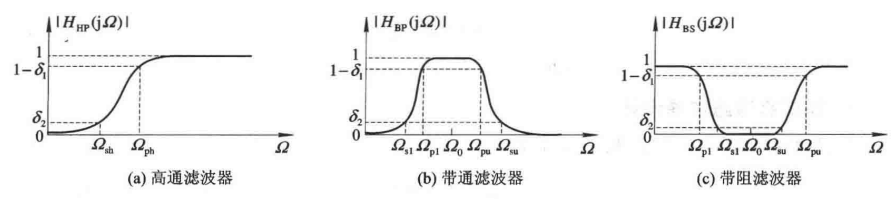
高通、带通和带阻滤波器的幅频响应曲线以及边界频率如下图所示：

从原理上讲，通过频率变换公式，可以将模拟低通滤波器的系统函数变换成希望设计的低通、高通、带通和带阻滤波器系统函数。设计过程中涉及的频率变换公式和指标转换公式较为复杂，其推导更为复杂。在本文不作介绍。

6、典型滤波器MATLAB设计

本节介绍一些常用的滤波器设计MATLAB代码

6.1 低通滤波器设计

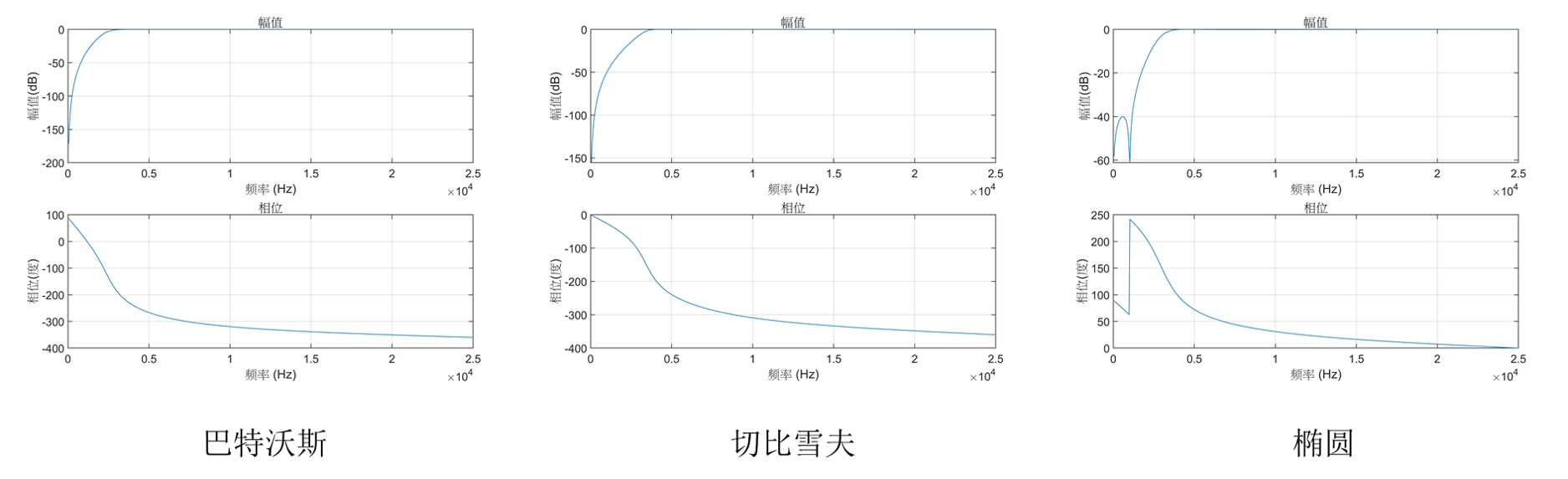
已知通带截止频率$f_p$=5kHz，通带最大衰减$\alpha_p$=2dB，阻带截止频率$f_s$=12kHz，阻带最小衰减$\alpha_s$=30dB。设计低通滤波器。

1、巴特沃斯滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=5000/(fs/2);ws=12000/(fs/2);
Rp=2;As=30;%设置滤波器参数
[N,wc]=buttord(wp,ws,Rp,As);%计算滤波器阶数N和3dB截止频率wc
[B,A]=butter(N,wc,'low');%计算滤波器系统函数分子分母多项式系数,low表示低通
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

2、切比雪夫滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=5000/(fs/2);ws=12000/(fs/2);
Rp=2;As=30;%设置滤波器参数
[N,wpo]=cheb1ord(wp,ws,Rp,As);%计算切比雪夫Ⅰ型滤波器阶数N和通带边界频率wpo,注意不是L是数字1
[B,A]=cheby1(N,Rp,wpo,'low');%计算滤波器系统函数分子分母多项式系数,low表示低通
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

如果使用切比雪夫Ⅱ型滤波器则将cheb1ord换成cheb2ord；cheby1换成cheby2。

3、椭圆滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=5000/(fs/2);ws=12000/(fs/2);
Rp=2;As=30;%设置滤波器参数
[N,wpo]=ellipord(wp,ws,Rp,As);%计算椭圆滤波器阶数N和通带边界频率wpo
[B,A]=ellip(N,Rp,As,wpo,'low');%计算滤波器系统函数分子分母多项式系数,low表示低通
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

6.2 高通滤波器设计

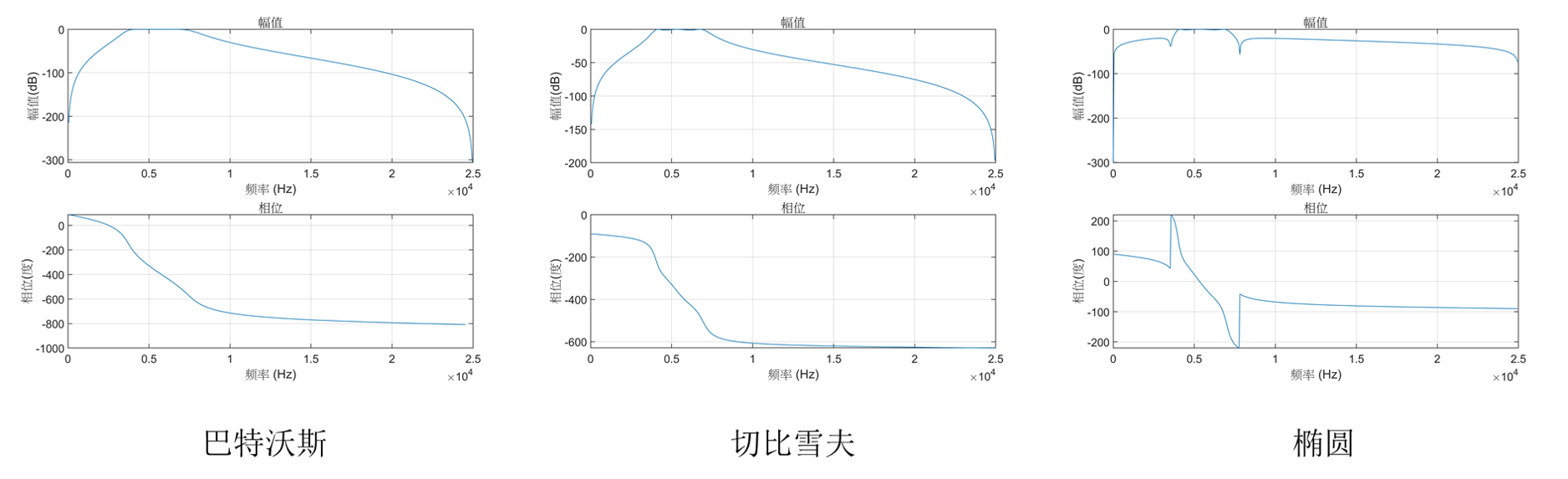
已知通带边界频率$f_p$=4kHz，通带最大衰减$\alpha_p$=0.1dB，阻带边界频率$f_s$=1kHz，阻带最小衰减$\alpha_s$=40dB。设计高通滤波器。

1、巴特沃斯滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=4000/(fs/2);ws=1000/(fs/2);
Rp=0.1;As=40;%设置滤波器参数
[N,wc]=buttord(wp,ws,Rp,As);%计算滤波器阶数N和3dB截止频率wc
[B,A]=butter(N,wc,'high');%计算滤波器系统函数分子分母多项式系数,high表示高通
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

2、切比雪夫滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=4000/(fs/2);ws=1000/(fs/2);
Rp=0.1;As=40;%设置滤波器参数
[N,wpo]=cheb1ord(wp,ws,Rp,As);%计算切比雪夫Ⅰ型滤波器阶数N和通带边界频率wpo,注意不是L是数字1
[B,A]=cheby1(N,Rp,wpo,'high');%计算滤波器系统函数分子分母多项式系数,high表示高通
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

3、椭圆滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=4000/(fs/2);ws=1000/(fs/2);
Rp=0.1;As=40;%设置滤波器参数
[N,wpo]=ellipord(wp,ws,Rp,As);%计算椭圆滤波器阶数N和通带边界频率wpo
[B,A]=ellip(N,Rp,As,wpo,'high');%计算滤波器系统函数分子分母多项式系数,high表示高通
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

6.3 带通滤波器设计

设计带通滤波器，要求通带上、下边界频率分别为4kHz和7kHz，阻带上、下边界频率分别为2kHz和9kHz，通带最大衰减为1dB，阻带最小衰减为20dB。

1、巴特沃斯滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=[4000,7000]/(fs/2);ws=[2000,9000]/(fs/2);
Rp=1;As=20;%设置滤波器参数
[N,wc]=buttord(wp,ws,Rp,As);%计算滤波器阶数N和3dB截止频率wc
[B,A]=butter(N,wc,'bandpass');%计算滤波器系统函数分子分母多项式系数,bandpass表示带通
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

2、切比雪夫滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=[4000,7000]/(fs/2);ws=[2000,9000]/(fs/2);
Rp=1;As=20;%设置滤波器参数
[N,wpo]=cheb1ord(wp,ws,Rp,As);%计算切比雪夫Ⅰ型滤波器阶数N和通带边界频率wpo,注意不是L是数字1
[B,A]=cheby1(N,Rp,wpo,'bandpass');%计算滤波器系统函数分子分母多项式系数,bandpass表示带通
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

3、椭圆滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=[4000,7000]/(fs/2);ws=[2000,9000]/(fs/2);
Rp=1;As=20;%设置滤波器参数
[N,wpo]=ellipord(wp,ws,Rp,As);%计算椭圆滤波器阶数N和通带边界频率wpo
[B,A]=ellip(N,Rp,As,wpo,'bandpass');%计算滤波器系统函数分子分母多项式系数,bandpass表示带通
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

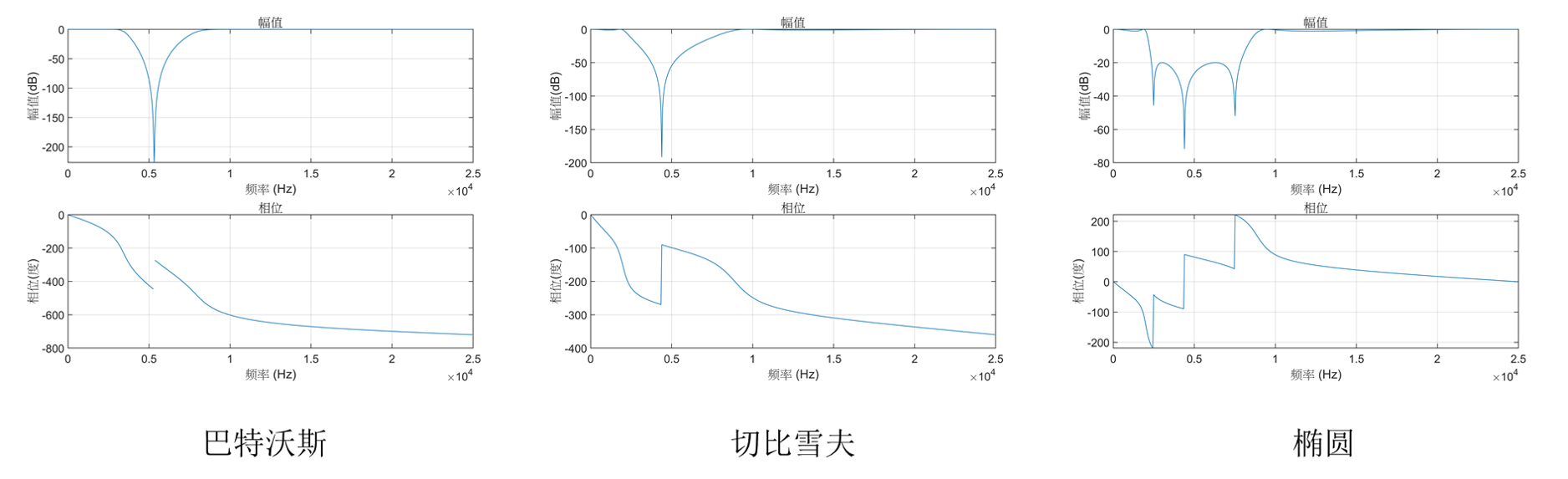
6.4 带阻滤波器设计

设计带阻滤波器，要求阻带上、下边界频率分别为4kHz和7kHz，通带上、下边界频率分别为2kHz和9kHz，通带最大衰减为1dB，阻带最小衰减为20dB。

1、巴特沃斯滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=[2000,9000]/(fs/2);ws=[4000,7000]/(fs/2);
Rp=1;As=20;%设置滤波器参数
[N,wc]=buttord(wp,ws,Rp,As);%计算滤波器阶数N和3dB截止频率wc
[B,A]=butter(N,wc,'stop');%计算滤波器系统函数分子分母多项式系数,stop表示带阻
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

2、切比雪夫滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=[2000,9000]/(fs/2);ws=[4000,7000]/(fs/2);
Rp=1;As=20;%设置滤波器参数
[N,wpo]=cheb1ord(wp,ws,Rp,As);%计算切比雪夫Ⅰ型滤波器阶数N和通带边界频率wpo,注意不是L是数字1
[B,A]=cheby1(N,Rp,wpo,'stop');%计算滤波器系统函数分子分母多项式系数,stop表示带阻
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

3、椭圆滤波器

%% 设计滤波器
fs=50000;%采样频率50kHz
wp=[2000,9000]/(fs/2);ws=[4000,7000]/(fs/2);
Rp=1;As=20;%设置滤波器参数
[N,wpo]=ellipord(wp,ws,Rp,As);%计算椭圆滤波器阶数N和通带边界频率wpo
[B,A]=ellip(N,Rp,As,wpo,'stop');%计算滤波器系统函数分子分母多项式系数,stop表示带阻
%% 展示幅频函数或损耗函数
freqz(B,A,[],fs)%画出幅频曲线和相频曲线

上述介绍的所有滤波器，输出结果为滤波器系统函数分子分母多项式系数。之后可以调用MATLAB的filter函数对输入信号进行滤波。

%% 通过滤波器后的输出信号
dataOut=filter(B,A,dataIn);%dataIn是输入信号